PC043356

(3.

RozdziałFimkcje jednej zmiennej

TwraitDzeNR 3.26. (Twierdzenie o pochodne/ superpozycji) JcśH funkcja f jest różniczkowalna w punkcie xq, a funkcja g w punk to funkcja go f jest różniczkowalna w .to. a jej pochodna jest równa

(g ° /)'(*o> = g'(f(xo»f'(x₀).

Przykład 335.

Niech a > 0 będzie ustaloną liczbą. Dla x e R mamy o* = e^x,na i dlatego

(er*)' = (ć^x>nay = e^xtafl • ln o = er* In a.

Twierdzenie 3.27. (Twierdzenie o różniczkowa i.ności funkcji odwrotnej)

Jeśli funkcja f : (d,b) —» (c,d) jest różniczkowalną suriekcją (tj. f((a,b}_: (c,d)j oraz f'(x) / 0 dla każdego * 6 (a, bj, to / jest bijekcją, a pochodu funkcji odwrotnej /“¹: (c, d) —> (a, Z?) wyraża się wzorem

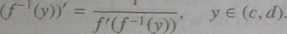
Przykład 336.

a) Funkcja/: (-f, f) —»(-1.1), f(x) = sinx, spełnia założenia twierdzenia3.27,Są

(arc siny)' =

siny)''S:'p-    ye(-l,l).

cos(arc siny)

Korzystając Z faktu, iż dla a e (-£, |), mamy cos o = +Vl - sin² o- i dlatego

(arc siny)' =

ijl — sin²(arc siny) ^ ^

Analogicznie rozważamy funkcję/: (~|, |) —» /?. /(jc) = tgx. Korzystając ze ran (3.14) i faktu, że (tg*/ = łatwo wyznaczyć

(arc tgy)' = cos² (arc tgy), y e /?. Ponieważ cos² a =    , więc ostatecznie

(arc tgy)' = y- y 6 /?.

Podobnie można wyznaczyć pochodne pozostałych funkcji tego typu:

(arceosy/ = —, — . y €(—1,1)*

^1-y²

(arc ctgyj' = -

t>) Obliczymy pochodną funkcji odwrotnej do f\R~* (0;«>y, /{*) * e*. Pochodna ta jest równa

Twierdzenie 3.28. (Twierdzenie Lag rangę’a)

Jeśli funkcja / jest ciągła na przedziale (a,b) i różniczkowalna na przedziale (a, b), gdzie a < b, to istnieje taki punkt xp e (a,b), że

mmmm

b — a

0.15)

Teza ostatniego twierdzenia oznacza, iż istnieje liczba 6 e (0,1). te

f(b) = /(o) + (b- a)f'(a + 9(b - a)).

Przykład 337.

Niech 0 < a < b. Pokażemy, że

Istotnie, przyjmując f(x) = \nx,z twierdzenia Lagrangs'a wynika, że istnieje c 6 (a.b), że In b-In a = ^(b - a). Wystarczy zauważyć, że )nb - Ina =fn(|i oraz £ < * <

Definicja 3.16.

Pochodną drugiego rzędu (drugą pochodną) funkcji /: (a,b)-* R nazywamy funkcję /" = (/')', o ile taka funkcja istnieje.

Pochodną rzędu n (gdzie n g N) nazywamy funkcję f*\x) = (/''■"(*))'. o ile istnieje. Przyjmujemy = /.

Przykład 3J8.

Niech /i będzie ustaloną liczbą naturalną. Dla funkcji f(x) = .rT\x eK. mamy

/'(.r) =

/"(.r) = n(/r - l)***².

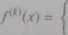
n(n-!)...(«-*+U*"^-* dbk<n.

0

dla ż > «■

Wszystkie te pochodne są określone na zbiorze J?.

123