PC043367

Roidżiat ***** jednej zmiennej

jest równe

X ^^(x) ~ «C*))<Łr.

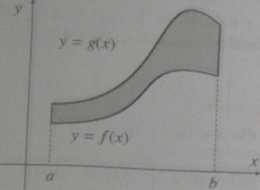
Rys. 3.10. Pole obszaru ograniczonego krzywymi o równaniach * = a, * ₌ b y = f(x) jest równe £(f(_x) - *(*» d*

Zrfidlo: opracowuje własne

Przykład 3.63.

Obliczymy pola P wybranych obszarów.

a> Obszar ograniczony krzywymi y = Ax^l\y = Ax. Mamy

^P= f ^4xdx ~ f 4jc²<Lc = 4 Ij^l - 4 - I*³!¹ = 2 - ^ = f.

"0    «A)    2 lo    3 lo 3 3

b) Obszar ograniczony wykresem funkcji y = cosjc oraz prostymi o równaniach y=0. x = | i x = —f. W tym przykładzie pole figury wyraża się wzorem

^{P =} Jl*^COSX<bc= = sin (I) ” ^sin (~ f) = ²-

fw/ERDZENTE 3.48. (TWIERDZENIE O WARTOŚCI ŚREDNIEJ)

Jeżeli / jest funkcją ciągłą na (tf, b), gdzie a < b, to istnieje taki punkt c 6 (a,b), żć

fW=ir-z I f<^x>^dx-    H

Liczbę po prawej stronie wzoru (3.32) nazywamy wartością średnią funkcji / na przedziale (a, ty.

Przykład 3.64.

Wartość średnia funkcji f(x) = siax, x € <0, n), jest równa

i r .    .    2

— I smrdt = —. zr Jo    *

A

Twierdzenie 3.49. (Twierdzenie o całkowanei w/t/ mwrr»wtiwi»i jeżeli flinkcja g: <a, f>)    <<*. d) jest różnlczkowałna w sposób ciągły ftfi (a.h),

a funkcja f; (c,d) -* R jest ciągła, to funkcja f(g(x)) • /(x) jest całkowalr# i zachodzi wzór

f

figix))ćix)4x ~ I f(yUy. Jgftf)

Przykład 3.65. Obliczając całkę

sin² xcosxdx,

przyjmujemy y = g(x) = sin x, stąd dy = cos* dr. Wyznaczamy granice całkowania: g(0) = sinfO> = 0 oraz ^(f}= sin^) = I. Zatem

2    /*1    yj ¹

sin²xeosxda: = I y² dy = — = o    Jo

1

3'

Można byłoby wyznaczyć najpierw funkcje pierwotne

If²

xcosxdx = ^ sin³ x + c.

skąd całka jest równa | sin³ xf₀^r2 = 1/3, czyli tyle samo, co poprzednio.

3,5.3. Całki niewłaściwe

Omówimy teraz całki, w których przedział całkowania jest nieograniczony.

Definicja 3.25.

Niech / będzie funkcją całkowalną na każdym przedziale (a, z), gdzie z> a. Jeżeli istnieje liczba

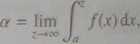
(333)

to mówimy, że / jest całkowalna na (a, oo). Mówimy, że całka

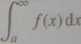
(3.34)

jest zbieżna, a liczbę a nazywamy wartością tej całki. Jeśli granica w (3.33) jest równa ±oo lub nie istnieje, to mówimy, że całka (3.34) jest rozbieżna. Analogicznie definiujemy całkę funkcji ciągłej / określonej w przedziale

(~oo,b):

j* f(x)dx = hrn^j^f(x)dx.

(3.3$)

145