PC043406

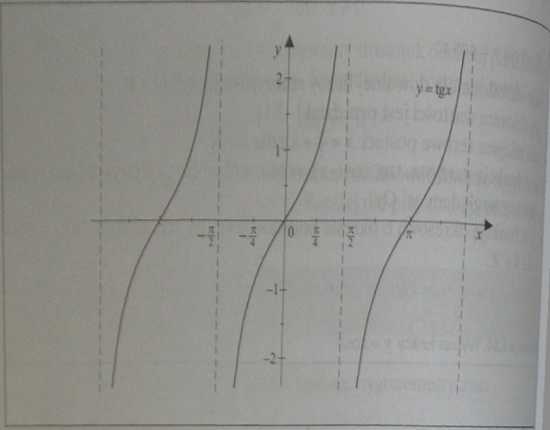
■•uniccjay »tgjc:

•    jest określona dla ¹$+£&, gdzie te Z, czyli -OaR\{«₊^.

•    przyjmuje wartości ze zbioru liczb rzeczywistych,

•    ma miejsca zerowe postaci x=kn dia ke Z,

•    jest funkcją przedziałami rosnącą,

symetiyczny względem początku układu,

•    jest funkcją okresową o okresie podstawowym tc, tzn. tg(² ₊ L

ke Z,    ²lfi

•    posiada asymptoty o równaniu postaci x=y+kn, gdzie k_€ i

•    jest funkcją nieparzystą, tzn. tg(-^r) = -tgx, wobec czego j_ej |

svmetrvcznv wzeledem ooczatku układu.    ^J Mrl

Ilustracja 1.65. Wykresu funkcji y=tg*

Funkcja.)?=ctg*:

Ilustracja 1.66. Wykres funkcji y = ctg*

W tabeli 1.4 podano wartości funkcji trygonometrycznych dla wybranych argumentów, natomiast w uwadze 1.37 przedstawiono wybrane wzory określające związki między funkcjami trygonometrycznymi.

Tabela 1.4. Wartości funkcji trygonometrycznych dla wybranych argumentów

	0		4 >	3	JK
y = sin*	0	i T	Jy	#	l
y = coś*	11	u 2	2	• } •	0 _
y = tg*	0	>/3 -3:. ”	1	fi	me istnieje [
y=ctg*	nie istnieje	S	1	& . 3	0

1

•    ma miejsca zerowe postaci x=j+kit dlake Z,

•    jest funkcją przedziałami malejącą,

•    jest funkcją nieparzystą, tzn. ctg(-²) = -ctg², wobec czego jej wykres J| symetryczny względem początku układu,

•    jest funkcją okresową o okresie podstawowym tc, tzn. ctg(²+kit) = ke Z,

•    posiada asymptoty o równaniach postaci²=kn, gdzie ke Z.

2

   jest określona dla^{2 2} kn, gdzie ke Z, czyli D=R \{kn: ke Z},

•    przyjmuje wartości ze zbioru liczb rzeczywistych,