104060

n wraz ze zmianą A mogą być opisywane w różny sposób. Dyspersja cząstkowa An=n_X2-n_i] jest określana dla pewnego przedziału widma AX=X₂-X_l. Zaś dyspersja materiału to An/AX. Określa się też tzw. dyspersję średnią:

Jn_pc=nF-nc    lub    An_¥._c=n_F - nc-    (2)

gdzie wskaźniki literowe oznaczają odpowiednie symbole linii widmowych. Współczynniki dyspersji (liczby Abbego) opisane są jako:

u, = ⁿ*~^!    _v = ⁿ^~¹

ⁿF~ ⁿc    łub    ^{d n}F~ⁿC.    (3)

Analityczne zmiany współczynnika załamania opisuje się różnymi zależnościami np. za pomocą wzoru Hartmanna:

nCO = n_c +

C

CA-A₀)“ _t

(4)

gdzie no, ^ c i a są wielkościami charakteryzującymi ośrodek i wyznaczane są jeżeli znamy współczynniki załamania dla wielu długości fal. Funkcje opisujące krzywe dyspersji nie są ciągłe w całym zakresie widma. Nieciągłości występują dla obszarów pochłaniania! Dla zakresu widma wolnego od zakresów pochłaniania można dyspersję opisać jako:

n(A)* = A₀ +

y

Z,A*-A*,

(5)

gdzie A_m określa długości wielu linii absorpcyjnych, lub wzorem Cauchy’ego:

nCA)³

(6)

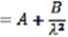
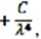
gdzie A, B, C są stałymi doświadczalnymi, które wyznacza się mierząc n dla 3 lub większej liczby długości fali A. Dla szkieł optycznych opisuje się zwykle dyspersję jako:

(7)

n(A)² = A_% +    + A₂A~² + A₉X+ + A_ĄA~* + A₅Ź"“

gdzie współczynniki Ą podawane są w katalogach szkieł obok wielu innych danych, lub wzorem Herzbergera: