Pytania wzorcowe 4

11. Stosując metodę iteracji prostej rozwiąż poniższe równanie, wymagana dokładność e =

0.01. Należy przyjąć, że rozwiązanie znajduje się w przedziale [0,6].

x³ - x - 2 = 0.

12. Stosując metodę iteracji prostej rozwiąż poniższe równanie, błąd przybliżenia 8 = |f(x₍k)) | < 0.01. Należy rozpocząć obliczenia od x«» = 6.

x³ - x - 2 = 0.

13. Stosując metodę iteracji prostej rozwiąż poniższe równanie, wymagana dokładność e = 0.01. Należy przyjąć, że rozwiązanie znajduje się w przedziale [0,5].

x³ - 2x - 4 = 0.

14. Dane jest równanie

x³ - 4x - 2 = 0.

Sprawdź, czy któreś z proponowanych poniżej postaci tego równania spełnia warunki zbieżności dla metody iteracji prostej w przedziale [0,5]

X =

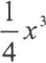
2

x = V 4x + 2

Jeżeli któreś z równań spełnia warunki zbieżności, oblicz X(3). Wykreśl w układzie współrzędnych kolejne iteracje na przebiegu obu funkcji.

Rozwiązywanie układu równań nieliniowych metodą Newtona-Raphsona.

1.    Układ równań przekształć do postaci iteracyjnej (k=0) dogodnej do rozwiązywania zgodnie z metodą Newtona-Raphsona dla X|«» = 2, X2«» = 3.

Xi X2 + 2 X2 - 6 = 0 xi + X2² - 5 = 0

2.    Zapisz wyrażenia na pochodne cząstkowe dla poniższego układu równań; oblicz wartości funkcji i pochodnych dla X]₍o) = 2, X2(o) = 3.

Xi X2 + 2 X2 - 6 = 0 xi + X2² - 5 = 0

3.    Opisz metodę Newtona-Raphsona rozwiązywania układu równań nieliniowych. Aproksymacja i interpolacja funkcji

1. Zaproponuj wielomian interpolacyjny Lagrange’a dla funkcji dyskretnej:

i	0	1	2
Xi	0	1	2
_Xi_	-2	0	4