P3200170

Mk---------------------1^25^L^5$

liczanie odległości między obiektami i a nowo utworzonym skupieniem p wedłu odległości większej (zob. rysunek 4.7).

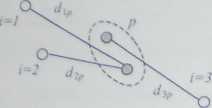
Rysunek 4.7. Zasada ustalania odległości w metodzie najdalszego sąsiada

Formalnie rzecz ujmując, w metodzie najdalszego sąsiada elementy macierzy odległości przekształca się sukcesywnie zgodnie z kryterium

(4.95)

d- = max(d^ ,d_u) zaś algorytm przeliczania odległości ma postać

(4.96)

Z wyjątkiem innej zasady przeliczania odległości między grupami, procedura postępowania jest tu analogiczna jak w poprzedniej metodzie, gdyż wynika z samej istoty grupowania hierarchicznego. A więc w każdym kolejnym kroku łączone są dwa obiekty bezwzględnie najbliższe, choć odległość jest ustalana według obiektu najdalszego w danym skupieniu. Jest to zatem procedura, która jest nastawiona na minimalizację największych międzygrupowych odległości (zob. rysunek 4.8).

O \

Rysunek 4.8. Odległość między skupieniami w metodzie najdalszego sąsiada

W przeciwieństwie do metody najbliższego sąsiada metoda najdalszego sąsiada skupia się na wewnętrznej spójności grup. Wykazuje ona tendencję do znajdowania grup spójnych, tworząc czasami kilka równoległych małych skupień. Obie metody, najbliższego i najdalszego sąsiada, ukierunkowane są na inne cele i zastosowane do tego samego zbioru danych dają zwykle znacznie różniące się re-

zultaly. Obie strategie są jednak czułe na występowanie jednostek oddalonych*" W przeciwieństwie do metody najbliższego sąsiada metoda najdalszego sąsiada wydłuża odległości (ang. spocę-dilaling) Obie metody, najbliższego sąsiada i naj dalszego sąsiada, są obecnie stosowane rzadko, ze względu na to że połączenia dwóch skupień na dowolnym etapie (poza pierwszym; są całkowicie określone przez mało reprezentatywne punkty w skupieniach, a nierzadko ekstremalne Bar dziej pożądane byłoby, aby skupienia reprezentowały jakieś punkty typowe (zob Pielou, 1984).

Przykład 4.4. (grupowanie hierarchiczne - metoda najdalszego sąsiada ■

Metoda najdalszego sąsiada zastosowana do macierzy odległości D * z przykładu 4.3 daje następujący dendrogram

Poziomy

Rysunek 4.9. Dendrogram (metoda najdalszego sąsiada

Sposób łączenia się obiektów. a zw łaszcza poziomy łączenia na dalszy ch eta pach, różnią się w tej metodzie od tego, co obserwowaliśmy w metodzie najbliższego sąsiada. Wyraźniejsze są tu skupienia: f 2,7). (1.3)oraz (4.5,6). Dzięki sięgnię ciu do odległości największych, poziom, na którym można by przerwać grupowanie hierarchiczne, jest łatwy do określenia (między 4.22 a 8,37). Nie znaczy to jednak, że w' tym konkretnym przypadku wykazaliśmy przewagę metody najdalszego sąsiada.

4.6.4. Metoda średniej grupowej

Kolejne strategie grupowania hierarchicznego mają na celu poszukiwanie pośredniej drogi między tym co daje strategia najbliższego sąsiada, a tym co zapewnia strategia najdalszego sąsiada.

Jednostka oddalona (ang outłiers).