s 187

187

187

7.3. Przyspieszenie punktów dała w ruchu płaskim

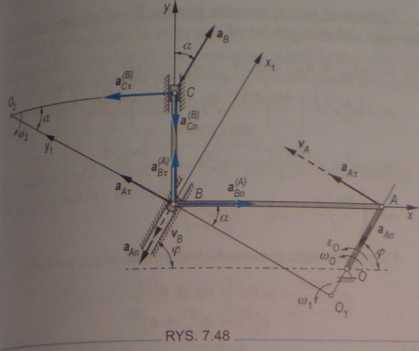
ROZWIĄZANIE Przyspieszenie punktu B

a_B = a _A+ *4^A) as a Ar + &An +

przy czym wektor JEJ jest skierowany od punktu B do punktu I a jego wartość jest równa

^a<Bn ~

Z rysunku mamy o>i = -    ; —-— = sina, stąd 0\A =

B V    Oi A    l

=/sina = czyli

	. (oor 2(Oo? , i - i
Żąłem	2
	CS V. nO fes 3 II CS
^ ^si? wzdłuż osi *i, więc suma rzutów ^^^^P$Jftzy8pieszenia na oś y\ jest równa zeru
1	p| + tt cos (p - a^(gj sin <p — 0

<|<>li I m ! Mg .S-^or

COSę>    /