skan0029 (3)

32 Stany skupienia materii

b =

RT,

8,314 • 33,3

8p_c    8 • 12,8 ■ 1,013 • 10⁵

= 26,7 10

-6

m

mol

0,0267

dm³

mol

Stąd

400 - 1,013 - 10⁵

ln tc = -^x

^v 8,314-300

26,7 • 10"⁶-

0,0249    (26,7 • H)-⁶) • 400 • 1,013 • 10⁵

8,314-300

+

2 • 8,314 • 300

= 0,3657.

Tak więc współczynnik lotności (p = 1,442, a sama lotność/= 584,4. Wyrażenie (2.29) można przekształcić do postaci

ln (p =

RT

J (^n - -y-)

gdzie zależność między/? i V_m wynika, w tym przypadku, wprost z izotermy Van der Waalsa.

Drugi sposób sprowadza się więc do wykreślenia wartości różnicy (V_m-RT/p) w funkcji ciśnienia (rys. 2.2), a następnie całkowania graficznego. Pole pod krzywą wynosi 199,16 J • mol^-1, obliczony stąd współczynnik lotności (p = 1,378, natomiast lotność/ = 558,5.

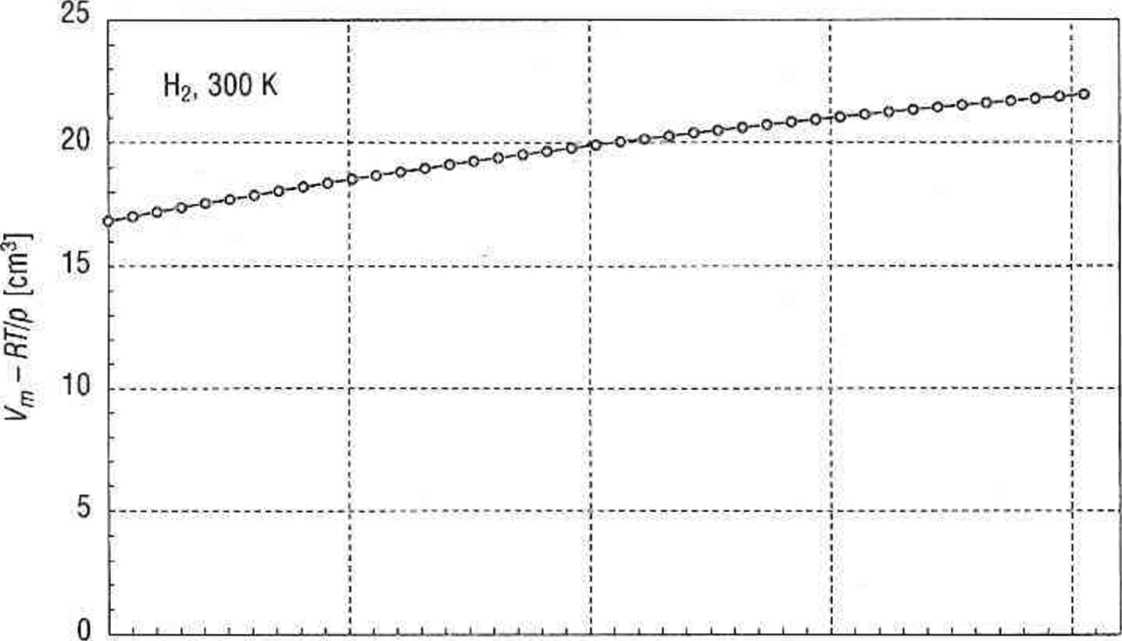
0    10    20    30    40

p [MPa]

Rys. 2.2. Wyznaczanie współczynnika lotności gazu metodą całkowania

graficznego

Wartości lotności wyznaczonej za pomocą równania wirialnego (ze współczynnikami obliczonymi z równania Van der Waalsa), a także otrzymanej metodą całkowania graficznego, przy wykorzystaniu tego równania, znacznie odbiegają od wartości doświadczalnych. Widać, że równanie Van der Waalsa źle odtwarza zachowanie się gazu rzeczywistego w wyższych ciśnieniach. ■