skan0160

Roztwory i równowagi fazowe 163

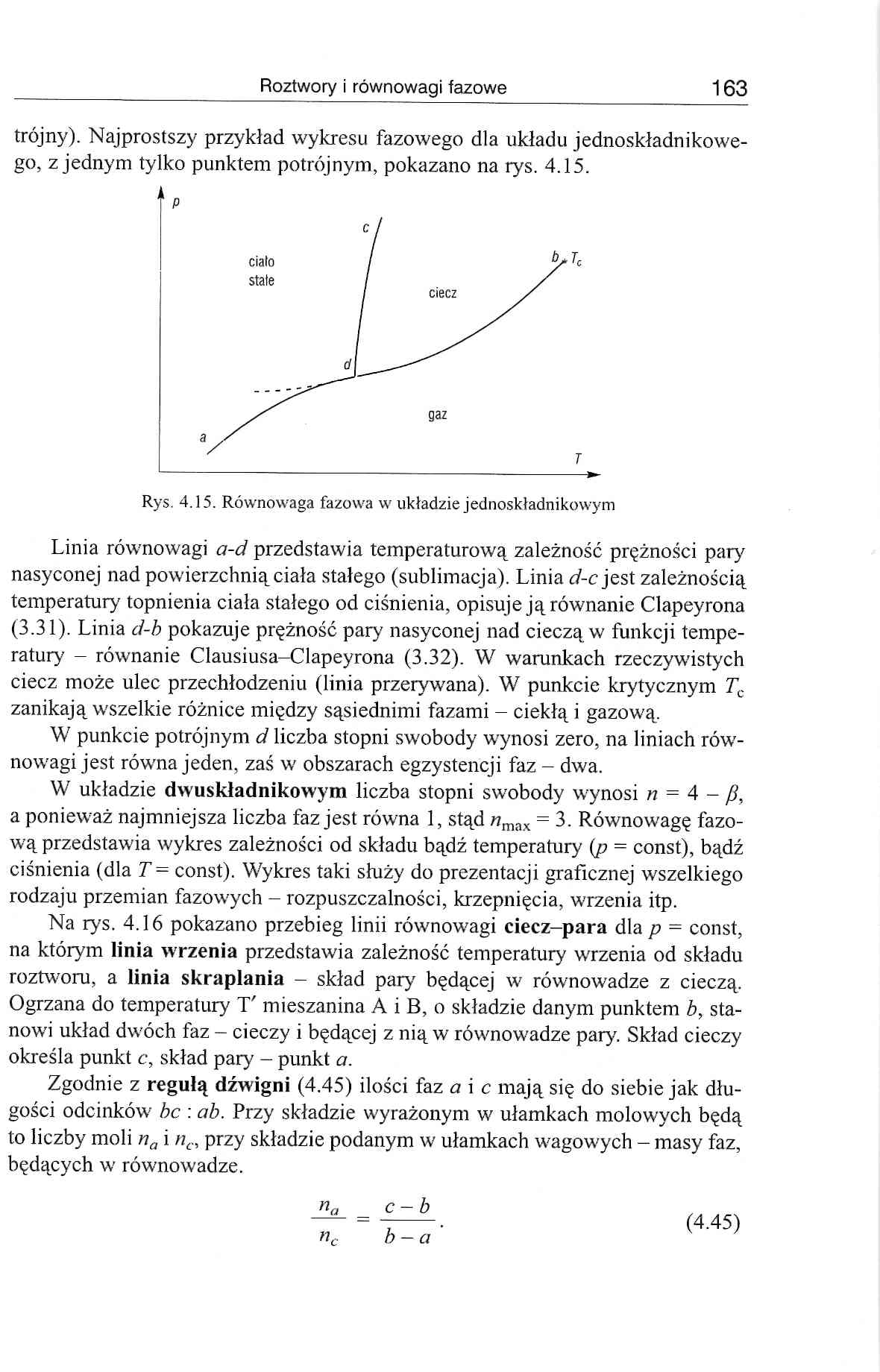
trójny). Najprostszy przykład wykresu fazowego dla układu jednoskładnikowego, z jednym tylko punktem potrójnym, pokazano na rys. 4.15.

Roztwory i równowagi fazowe 163

Linia równowagi a-d przedstawia temperaturową zależność prężności pary nasyconej nad powierzchnią ciała stałego (sublimacja). Linia d-c jest zależnością temperatury' topnienia ciała stałego od ciśnienia, opisuje ją równanie Clapeyrona (3.31). Linia d-b pokazuje prężność pary nasyconej nad cieczą w funkcji temperatur}' - równanie Clausiusa-Clapeyrona (3.32). W warunkach rzeczywistych ciecz może ulec przechłodzeniu (linia przerywana). W punkcie krytycznym T_c zanikają wszelkie różnice między sąsiednimi fazami - ciekłą i gazową.

W punkcie potrójnym d liczba stopni swobody wynosi zero, na liniach równowagi jest równa jeden, zaś w obszarach egzystencji faz - dwa.

W układzie dwuskładnikowym liczba stopni swobody wynosi n - 4-/3, a ponieważ najmniejsza liczba faz jest równa 1, stąd «_max = 3. Równowagę fazową przedstawia wykres zależności od składu bądź temperatury (p = const), bądź ciśnienia (dla T = const). Wykres taki służy do prezentacji graficznej wszelkiego rodzaju przemian fazowych - rozpuszczalności, krzepnięcia, wrzenia itp.

Na rys. 4.16 pokazano przebieg linii równowagi ciecz-para dla p = const, na którym linia wrzenia przedstawia zależność temperatury wrzenia od składu roztworu, a linia skraplania - skład pary będącej w równowadze z cieczą. Ogrzana do temperatury T' mieszanina A i B, o składzie danym punktem b, stanowi układ dwóch faz - cieczy i będącej z nią w równowadze pary'. Skład cieczy określa punkt c, skład pary - punkt a.

Zgodnie z regułą dźwigni (4.45) ilości faz a i c mają się do siebie jak długości odcinków bc : ab. Przy składzie wyrażonym w ułamkach molowych będą to liczby moli n_a i n_c, przy składzie podanym w ułamkach wagowych - masy faz, będących w równowadze.

(4.45)

b-a

n_a c-b ^fh