skan0220

Kinetyka chemiczna 223

Po jego scałkowaniu otrzymamy wyrażenie

c_B = akt cxp (-kt).    (5.32)

Maksymalne stężenie produktu pośredniego osiągnie się, gdy

' = f    (5.33)

Jeśli k_b » k_a (B natychmiast przechodzi w C), to wyrażenie (5.28) daje się łatwo przekształcić w

c_c = a(] - exp(~k_at)\    (5.34)

gdyż

K exp (~k_h t) < k_b exp (~k_a t).

W tym przypadku etapem decydującym o kinetyce całego procesu jest więc reakcja A —> B.

Przykład 5.10. Okresy połowicznego rozpadu izotopu ²9oTh i ^Pa wynoszą

²9oTh ²^Pa + (S    t\/₂ = 24,1 dni,

²9]Pa % ²l⁴2U + p    t_m = 6,75 h.

Wychodząc z 2000 atomów ²9oTh w chwili t = 0, obliczyć liczbę atomów Th, Pa i U po 12 h.

Rozwiązanie. Reakcja rozpadu Th jest reakcją następczą, której pierwszy etap opisany jest przez równanie (5.25)

N= N₀&xp(-k_at),

gdzie

ln 2

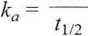
ln 2

24,1 • 24

1,198 • 10^_3łr^l.

Po czasie t = 12 h

JV_Th = 2000 • exp (-1,198 • 10^-3 • 12) = 2000 • 0,9857 = 1971 atomów.

Liczbę atomów Pa obliczymy z równania (5.27)

Npa ^-

Móka

k_b - k_t

(exp (~k_a i) - exp (~k_h t)).