68830 skan0219

222 Kinetyka chemiczna

Stąd po scałkowaniu mamy

222 Kinetyka chemiczna

^CB

k„ a

a

h - k

(cxp (-k_ał) - exp (~k_bt)).

(5.27)

a

Wstawiając to wyrażenie do (5.24c) można łatwo otrzymać

c_c = a\\ +

k_a exp (~k_h t) - k_h exp (~k_a /)

k_h-k

(5.28)

cl

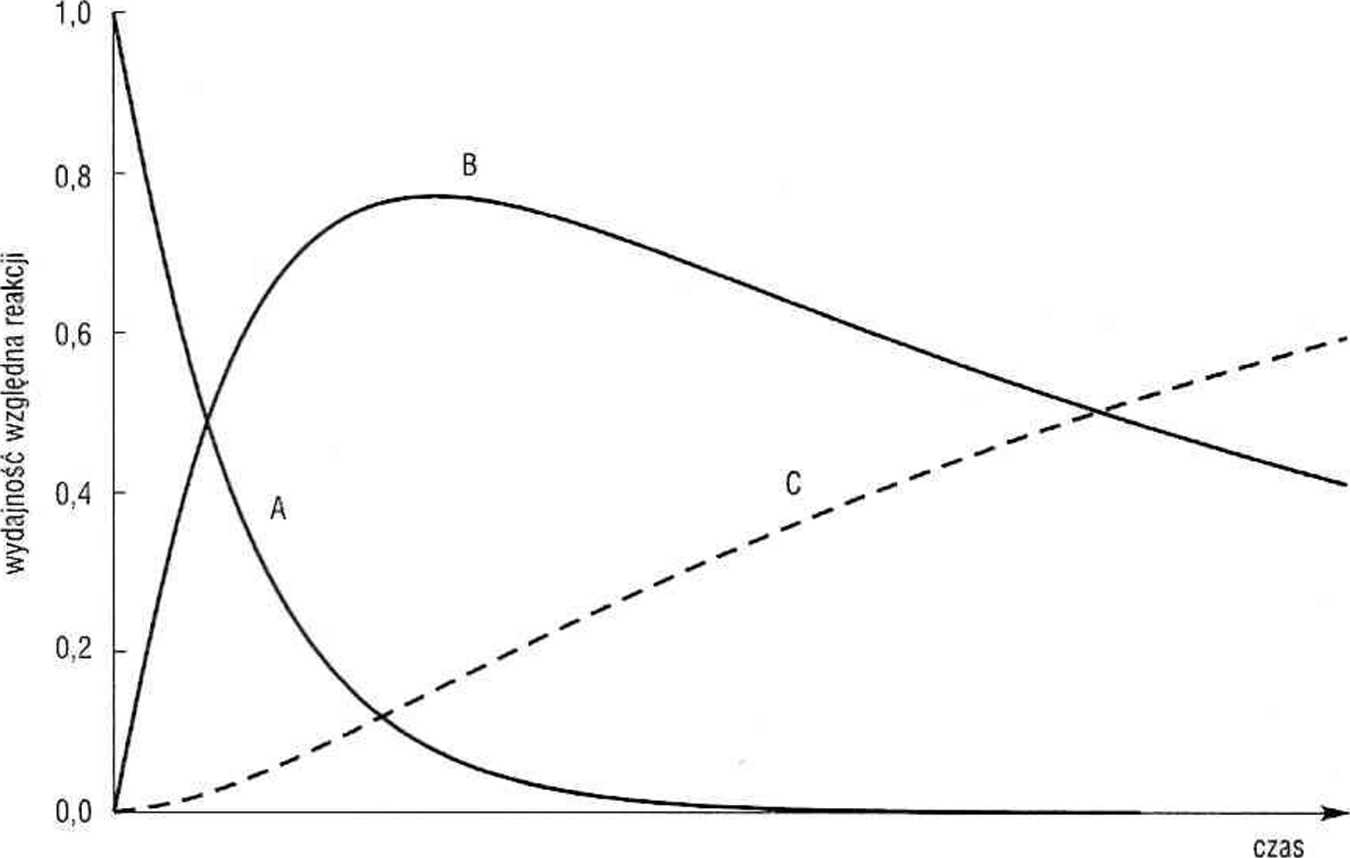
Stężenie B przechodzi przez maksimum (rys. 5.7).

ku kit

Rys. 5.7. Wydajność względna reakcji następczych typu A —» B —» C

Różniczkując równanie (5.27) względem t, z warunku, iż (dc_B/dt)_max = 0, znajdziemy czas, po którym uzyska się maksymalną wydajność produktu B:

ln (k_Q/k_b)

^max    /    /

A' - ki

(5.29)

a

a także samą wydajność maksymalną:

(^cB)max ^a

l- \kbkh ,~k_a) ^Ka

(5.30)

Gdy k_a = k_b = k, równanie (5.26) będzie miało postać

d

dt

(c_Bexp(A7)) = ka.

(5.31)