skan0215

218 Kinetyka chemiczna

Obliczoną stąd stałą szybkości k' = (1,22 ± 0,01) • 10 ⁸ Pa ¹ • s ¹ można wyrazić w zwyczajowo przyjętych jednostkach (M^-1 • s^-1)

k= k' RT• 10³ = 1,22 - lO”⁸ • 8314 - 523,15 - 10³ =

= (5,31 ±0,04)- 10"²M-’ -s"¹. ■

Jako reakcje odwracalne (przeciwbieżne) definiujemy te przemiany chemiczne, w których nie można zaniedbać procesu odtwarzania substratów przez reagujące ze sobą produkty

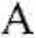
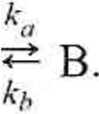
Dla uproszczenia przyjmijmy, iż obie reakcje są I rzędu. Ponadto załóżmy, że w chwili / = 0 składnik B jeszcze się nie utworzył, a w konsekwencji bilans stężeń reagentów wyraża się równaniem a = c_A + c_B, spełnionym w każdej chwili. Szybkość tej reakcji można opisać następująco:

cJcq

dt

K,Ca ~ K^cb = Kia - c_B) - k_bc_B = k_aa - (k_a + k_h)c_B.

(5.17)

W stanie równowagi, dla t = °<>₅ dc_Bidt = 0, a stężenie B = (c_B)_r, toteż

k_aa = (k_a +k_h)(c_B\.    (5.18)

Całkując (5.17) z warunkiem początkowym t = 0, c_B = 0, otrzymujemy

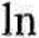
k_aa~(k_a + k_h)c_B k_aa

-~{k_a + k_h)t.

(5.19)

Jeśli podstawić (5.18) do równania (5.19), to otrzyma się, po uproszczeniu.

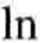
(CB)r

(^cb)t ~ ^CB

- (k_a + k_b)t

(5.20)

lub, korzystając z równania bilansu a = c_A + c_B, a zatem a = (e_A)_r + (c_B)_r,

a — (f/Or

Ca - (c_A)r

(K ⁺ K)^L

W niektórych podręcznikach, przez analogię do (5.13), suma (k_a + k_h) nazywana jest efektywną stałą szybkości reakcji.

Jeżeli dla t = 0, [B]₀ = ń, to równanie kinetyczne (5.17) przybierze postać

dc_B _ d(b + x) ~dt ~ dt

dx

dt

= k_a(a - x) - k_h(b + x),

(5.21)