47714 skan0253

256 Kinetyka chemiczna

szybkość powstawania produktu w funkcji [A] i stałych szybkości, przy założeniu stanu stacjonarnego dla A*.

W jakich warunkach jest to a) reakcja pseudopierwszorzędowa, b) pseudo-drugorzędowa? Odp. dcyjdl = Aą A'-,c\!{k_x + k_^c_A); a) duże stężenie substratu (MA] > Aą); b) małe stężenie substratu.

5b:6. Cyklobutanon, C₄H₆0, ulega termicznemu rozkładowi według dwóch równoległych reakcji I rzędu. Na podstawie poniższych danych, odnoszących się do 383°C i

t [min]		0,5	1,0	3,0	6,0
[C2H4]	10^5, M	0,31	0,68	1,53	2,63
[C3H6]	O k	0,21	0,47	1,24	2,20

C₄H₆0

_ c₂h₄ + c₂h₂o

c₃h₆ + co stężenia początkowego cyklobutanonu równego 6,5-10 ⁵ M, obliczyć stałe szybkości k] i k₂. Odp. A ] = (8,30 ± 0,27) • 10^-2 min^-1, k₂ = (7,21 ± 0,09) • 10^-4 min^-1.

5b:7. Reakcja bromowania nitrobenzenu do monobromopochodnej jest reakcją I rzędu. Po 67 minutach reakcji stężenie nitrobenzenu zmniejszyło się

0    20%. Produkt zawierał 4% (molowych) izomeru orfo, 74% izomeru meta i 22% izomeru para. Obliczyć stałe szybkości reakcji bromowania nitrobenzenu do odpowiedniej pochodnej.

Odp. k_orto = 1,33-10^-4; k_meta = 2,46 -10^-3; k_para = 7,33-10^-4 min^-1.

5b:8. Izotop ²§⁴Pb ulega rozpadowi fi, tworząc ²g⁴Bi, z którego, po dalszym rozpadzie fi powstaje ²x⁴Po. Czasy połówkowego rozpadu wynoszą dla ²g⁴Pb

1    ²^⁴Bi, odpowiednio, 26,8 min i 19,7 min. Obliczyć liczby atomów' Pb, Bi i Po po 30 minutach, jeżeli w chwili t = 0 było 1000 atomów' ²s₂Pb. Czy' liczba atomów- Bi może osiągnąć wartość 500? Odp. n_?b- 460, /7_Po= 228, /?_Bi = 312. Nie, («_Bj)_maks = = 313.

A'_a

5b:9. Produkt B powstaje w wyniku reakcji A —> B, a ten ulega rozkładowi

A ^

B —» C. Obie reakcje są I rzędu. Zakładając, że w chwili t = 0, [B]₀ = 0, obliczyć maksymalną wydajność względną, ([B]/[A]₀)_maks, oraz czas jej osiągnięcia, gdy 1) A_a = 0,4; A_b = 0,2 min^-1; 2) A'_a = 0,2; A_b = 0,4 min^-1; A'_a = A_b = 0,2 min^-1.

Odp. 1) 50%; 3,47 min; 2) 25%; 3,47 min; 3) 36,8%; 5 min.

5b:10. Rozważyć reakcję odwracalną (obie reakcje sąl rzędu)

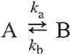
z warunkami początkowymi [A]₀ = a, [B]₀ = 0. Oznaczając dla dowolnego czasu /, [A] = a - x, [B] = x, wykazać, że