skan0232

Kinetyka chemiczna 235

Z różnicy obliczonych w ten sposób wartości energii aktywacji E_A(i) dla reakcji w obu kierunkach można obliczyć standardową zmianę energii wewnętrznej reakcji AU® = -20,9 kJ • mol^-1. Wynik ilustruje diagram energetyczny reakcji (rys. 5.10). ■

Zgodnie z teorią zderzeniową szybkość reakcji A + B —> produkty jest funkcją liczby zderzeń (Z_AB) i ułamka cząsteczek mających energię £_a, wystarczającą do przereagowania. Szybkość reakcji zależy od liczby zderzeń, w których wyniku powstaje produkt, w 1 m³ mieszaniny gazowej w ciągu 1 sekundy

v' = PZ_ABexp(- Jjr] [nr³ ■ s-¹],    (5.46)

gdzie P jest czynnikiem sferycznym wyrażającym prawdopodobieństwo właściwej orientacji w momencie zderzenia,

Zab =A^r(A).V(B)7C^_B*    (5.47)

jest liczbą zderzeń w ciągu 1 sekundy między cząsteczkami A i B zawartymi w 1 m³. N(A) i A^r(B) oznaczają, odpowiednio, liczby cząsteczek A i B w 1 m³, natomiast

^ab ^-

⁺

2

[m]

(5-48)

jest średnicą zderzeniową obu cząsteczek. Można przyjąć w uproszczeniu, że w ciągu 1 s z cząsteczką A zderzą się cząsteczki B zawarte w walcu o promieniu cr_AB i długości równej względnej prędkości średniej w - zob. (2.31):

w

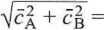
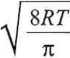
(    + M_b \

\ M_aM_b I

[m • s-¹].

(5.49)

Chcąc porównać v\ dane relacją (5.46), z szybkością reakcji v = £₂[A][B], wyrażaną zazwyczaj w M • s^_1, należy przeliczyć zarówno l?', jak i stężenia N(A) oraz N(B)

/

v

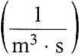
= 10³

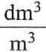
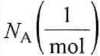
/ mol \ Idm³ • s /

podobnie N(A) = [A] • 10³ • N_A oraz jV(B) = [B] • 10³ • N_A.

Uwzględniając powyższe, możemy zapisać szybkość reakcji i/jako

v' = 10³ • N_av=P[A] • 10³ • jV_a[B] ■ 10³ • N_An<rl_Bwexp (- -Jjr] (5.50)