skan0347

350 Zastosowanie transformacji Lap!ace’a

Działając operatorem Laplace’a na równanie (17) i zakładając przemienność operacji różniczkowania z operatorem 9l\ otrzymamy

J

dc (-v, 0 dx

x=0

exp (-57) dt =

dC (x, s) dx

A—0

nFD

exp (-st) dt,

a zatem

dC (x, s)

j exp {-si)

dx    )x=o    nFZ)

Z przyrównania (19) i (20) możemy określić Cj:

j 1

5

(20)

(21)

nFD^1/2s^3/2

i po wstawieniu jej do równania (18) otrzymamy, nadal w przestrzeni obrazu,

7^ \

(22)

C (*, 5) = C₀ I — I +

exp \—x

s I nFD^m

,.3/2

/

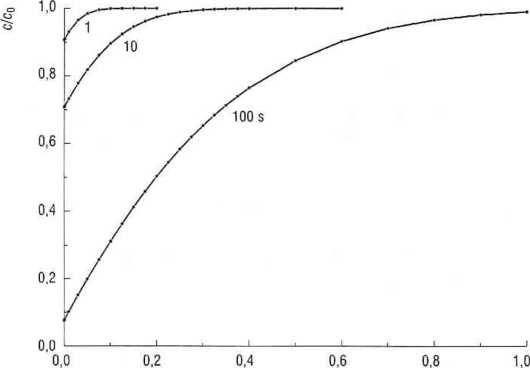
x, mm

Rys. D2.3. Profil stężeniowy dla warunku brzegowego określonego przez sposób prowadzenia elektrolizy (D = J • 10^-v m² • s^_1; c₀ = 40 mol • m^-3;/ = -20 A ■ m^-2)