skan0344

Zastosowanie transformacji Laplace’a 347

gdzie

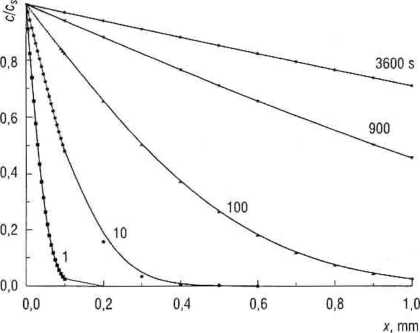
Rys. D2.1. Rozpuszczanie soli w zbiorniku w funkcji czasu i odległości od dna zbiornika

x

2 '

Przy obliczeniach korzysta się z tablic <P(y) lub z rozwinięcia tej funkcji w szereg

<£(>’) =

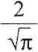
o

I

(_iyy,;+l (2)1 + 1)«!

gdzie wystarczy ograniczyć się do n = 100 (niezbędne jest zastosowanie prostego programu).

Nietrudno sprawdzić, wykonując proste różniczkowanie, że znaleziona funkcja c(.v, /) jest rzeczywiście całką rówmania (1)

dc (x, i) ~dt

^2CS 1	[ A-^2 '
£^expl	\ 4Dt,
xr^3!2	( x^2

4 VZ)

exp

3/2    -

2 xkD

4 Dl

d²c (x, i) dx²

C,

NnDt

2 Dl

exp

4 Dt

Zrozumiałe jest, że zarówmo sposób znajdowania całki równania (1), jaki jej postać w' istotny sposób zależą od przyjętych warunków. W przykładzie powyżej warunek początkowy wynosił zero. Nieco trudniej rozwiązuje się to równanie,