25323 skan0345

348 Zastosowanie transformacji Laplace’a

gdy jest on różny od zera, np. podczas elektrolizy, gdy początkowe stężenie jonów jest dla każdego x takie samo, toteż warunek początkowy wynosi

c(x, 0) = c₀    (10)

Przyjmijmy ponadto, że reakcja elektrodowa zachodzi szybciej niż dyfuzyjny dopływ jonów do powierzchni elektrody, toteż dla x = 0

c(0, /) = 0.    (11)

Teraz, działając operatorem Laplace’a na wyrażenie (1), dostajemy w przestrzeni obrazu, po uwzględnieniu warunku (10), niejednorodne równanie różniczkowe II rzędu:

d² C (x, 5)

s

D

C (x, s) +    = 0.

(12)

Jego rozwiązaniem ogólnym, znalezionym metodą przewidywania, jest funkcja

C(x, s) = -y + Cj exp |-x    + ^C2 ^exP    (¹³)

Łatwo sprawdzić, różniczkując funkcję C(x, s) że spełnia ona równanie (12). Ze względu na ograniczoność funkcji C(x, s) stała C₂ = 0, natomiast dla x = 0 rozwiązanie ogólne przechodzi w

Ć(0, s) = — + Ci = 0,

5

zatem

c,--a-

i rozwiązaniem równania (12) - czyli w przestrzeni obrazu - jest funkcja

exp -x

co

1

C (x, s)= — 1 - exp -x A —    = c₀ —

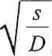
s

■    (14)

Po dokonaniu, tak jak poprzednio, transformacji odwrotnej otrzymamy wyrażenie

c(x, t) = se \c₀

1    exp(-£Ws)

s    s

= Co 1

\-0

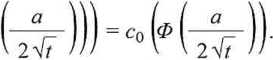
(15)