skanuj0195 (5)

9.3. Zasady obliczania wytrzymałości osi i wałów dwu pod porowych

Jak wynika z treści rozdziału 9.1, osie oblicza się na zginanie, a wały — na skręcanie z równoczesnym zginaniem lub (w nielicznych przypadkach) — tylko na skręcanie.

Obliczanie wytrzymałości osi i wałów polega na:

•    wyznaczeniu metodami statyki wszystkich sił czynnych (obciążeń) i biernych (reakcji podpór lub utwierdzeń) działających na oś lub wał;

•    obliczeniu wartości momentów zginających (dla osi i wałów) oraz skręcających i zastępczych (dla wałów) co najmniej dla punktów przyłożenia sił zewnętrznych i dla punktów podparcia (łożysk);

•    obliczeniu średnic wału w podstawowych przekrojach i ustaleniu kształtu wału (osi);

•    wykonaniu (w razie potrzeby) obliczeń sprawdzających (np. z u-względnieniem osłabienia wału lub osi karbami) i uzupełniających, polegających na obliczeniu sztywności wału itp.

Obliczanie osi dwupodporowych na zginanie. Oś oblicza się jako belkę podpartą na dwóch podporach (łożyskach) i obciążoną siłami skupionymi. Reakcje w podporach wyznacza się na podstawie warunków równowagi. W przypadku osi obciążonej tylko jedną siłą poprzeczną F (rys. 9.6a, b) reakcje oblicza się z zależności

b    a

Ra = F~, R_b = F-

77$	a	T	t	i_ _
	Ja l^F
	* a _		b
	t

Oś ruchoma

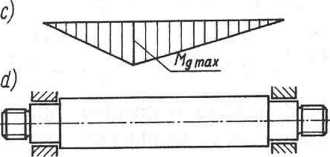
Rys. 9.6. Obliczanie osi na zginanie: a) schemat osi, b) schemat obciążenia, ć) wykres momentów zginających, d) oś gładka, e) teoretyczny kształt osi o równej wytrzymałości, f) rzeczywisty kształt osi schodkowej (wg di na rys. e)

Maksymalny moment zginający wynosi

(9.4)

M_g = R_A -a lub M_g = R_b b

Na podstawie warunku wytrzymałościowego na zginanie oblicza się minimalną średnicę osi

53* 195