str093 (5)

i

111. ODWZOROWANIA KONFOREMNE    93

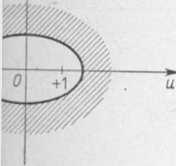
! ulegnie zmianie, a wnętrze koła 11.9) odwzorowuje konforemnie :lipsy (11.9'), a zewnętrze koła Su^l.

ezcłrt. Przyjmując w = u + tv, azdzieleniu części rzeczywistej

osx.

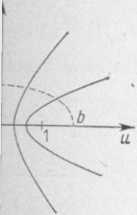
urojoną Ov (rys. 1.21), bo gdy t # 0, równoległa do osi uro-czyźnie zmiennej (w) w jedną

nązków (11.10').

Z równań (11.10') wynika dalej, że gdy y — 0 wówczas v = 0. Wobec tego odcinek -^7t<x<^it osi rzeczywistej w płaszczyźnie (z) przechodzi na płaszczyźnie zmiennej (u) w odcinek — 1 <u< 1 osi rzeczywistej. Natomiast każdy odcinek aa' równoległy do osi Ox przechodzi na płaszczyźnie zmiennej (vt) w półelipsę bb' o równaniu

(11.10"')

i(? + 0² + W-e-^yf

Oczywiście hiperbole (11.10") są ortogonalne do elips (11.10'"), bo są obrazami prostych x= const i y = const do siebie prostopadłych. Stąd wniosek: Funkcja (11.10) odwzorowuje konforemnie pionowy pas nieskończony — £;t<Rez<-iji na całą płaszczyznę zmiennej (w) rozciętą wzdłuż dwóch odcinków l<i/<oo oraz — oo<«< —1 osi rzeczywistej.

Uwaga. Analogicznie, na tak rozciętą płaszczyznę zmiennej (w) funkcja (11.10) odwzorowuje każdy pas pionowy

(2/c—l)i7t<Rez<(2k+ 1)^71, k = 0,±l,±2,...

Twierdzenie 8. DługośćL obrazu krzywej C o równaniu z = "(/), a^t^b. przy odwzorowaniu konforemnym w = f(z) wyraża się następującym wzorem:

oni)    wimoMoi*.

a

Twierdzenie 9. Pole S obrazu obszaru D przy odwzorowaniu konforemnym iv = /(-) wyraża się wzorem:

(11.12)    S = tf\f'(z)\²dxdy.

D

B. Funkcja Greena i jej związek z funkcją odwzorowującą

Definicja 8. Niech D będzie dowolnym obszarem (ograniczonym lub nie, jedno-spójnym lub wielospójnyin), C jego brzegiem, wreszcie z₀ = x₀ + iy₀ niech oznacza dowolny punkt obszaru D (nie wykluczamy przypadku z₀ = oo). Mówimy, że funkcja rzeczywista G(z) = G(x,y) dwóch zmiennych rzeczywistych x i y określona w obszarze D jest funkcją Greena dla obszaru D z biegunem w punkcie z₀, jeżeli spełnia ona 3 następujące warunki:

1° jest harmoniczna i dodatnia w obszarze D z pominięciem punktu z₀,

2° dąży do zera, gdy punkt z = x+iy dąży do brzegu C,

3° różnice

1

(11.13)    G(z)-log--- dla z₀^oo,

Iz-^ol

(11.13')

G(z) —log|z| dla z₀ = oo

dążą do granicy skończonej, gdy z->z₀. Często zamiast G(z) piszemy G(z, z₀) dla zaznaczenia, że punkt z₀ jest biegunem funkcji G(z). Z warunku 3° wynika, że

G(z,z₀)~>co, gdy z->z₀.

/