Untitled Scanned 128

130

ZADANIA ZAMKNIĘTE

962.

963.

RACHUNEK PRAWDOPODOBIEŃSTWA

Liczba punktów, których odcięta należy d*» zbioru {I, 2, 3. 4. 5, 6}, a rzędna do zbioru {50, 51, 52. 53), jest równa

a) 6 + 4;    b) 6-4;    c) Ó-6-6-6;    d) 4-4-4-4-4-4.

Liczb naturalnych dwucyfrowych o różnych cyfrach, większych od 36 jest

a) 21;    '    b) 54;    '    c) 57;    d) 63.

964.

Ze zbioru {1, 2. 3. 4, 5, 6. 7. 8) losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe

d)

5. 8 ’

965.

W pudelku znajdują się tylko kule białe i czerwone. Stosunek liczby kul białych do liczby kul czerwonych jest równy 2:3. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania białej kuli jest równe

a)

1.

5’

b) f;

^d> t

966.

Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo wyrzucenia co najmniej raz liczby oczek podzielnej przez 3 jest równe

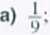
d)

5

9‘

967.

Prawdopodobieństwo zdarzenia /\ jest 7 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do zdarzenia A. Wobec tego prawdopodobieństwo zdarzenia A jest równe

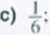
d)

968.

Zdarzenie A u tl jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia A n B jest równe 0.25. Wobec tego suma prawdopodobieństw zdarzeń A i li jest równa

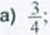
b)

4.

5’

c) l;

d)

5 4 ’

969.

970.

Zdarzenia A i B są podzbiorami zbioru zdarzeń elementarnych 12. Wiadomo, że P(A kj B) + P(A n li) = 1 Zatem

a) P(A) € (0; I);    b) P(A n li) €(();!); c) P(A \ B) <= (0; I); d) P(B) e (0; 1).

Prawdopodobieństwo zdarzenia A jest równe L a prawdopodobieństwo sumy zdarzeń A i B jest równe |. Wobec tego prawdopodobieństwo zdarzenia B\A jest równe

a)

b) 1;

=) i;

^d> f

Z grupy dzieci wybieramy losowo dwoje. Prawdopodobieństwo wybrania co najmniej jednej dziewczynki jest równe j^.a prawdopodobieństwo wybrania co najwyżej jednej dziewczynki jest równe Wobec tego prawdopodobieństwo wybrania dwóch dziewczynek jest równe

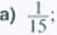
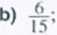
d)

ii

15'

971.