Image52

102

2.43. Rozpatrzmy ciało o masie m całkowicie zanurzone w cieczy. Niech m_c oznacza masę cieczy o objętości równej objętości tego ciała. Przesunięcie ciała

z położenia a do położenia b (rys.33) jest równoznaczne

• »

- b-

-<----»

* m * i " c «

Z\___j

Rys.33

zamianie miejscami mas m i m_c.

W stanie początkowym energia potencjalna tych dwu elementów obliczona względem dowolnego ustalonego poziomu (np. dna naczynia) jest równa

E_pi = mgh_l + m_cgh₂, a w stanie końcowym

ważna

Ep2 = mgh₂ + m_cgh_t.

rzymana stąd zmiana energii układu jest równo pracy wykonanej podczas przesunięcia ciała, tzn

(m

m_c) g Ah = FAh.

Mamy więc

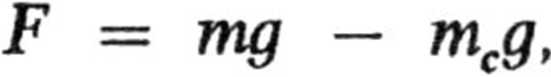
II

edesa.

co stanowi treść prawa Archi

2.44. Jeżeli wydłużenie sprężyny oznaczymy sy energia potencjalna układu

II

bólem x, to całkowita

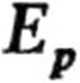
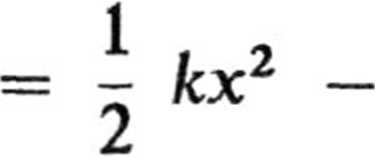
mgx,

gdzie: ~ kx² 2

mgx

-    energia potencjalna siły sprężystości,

-    grawitacyjna energia potencjalna liczona względem poziomu wyznaczonego przez dolny koniec wiszącej swobodnie, nieobcią-żonej sprężyny.

Warunkiem ekstremum jest

dĘp

dx

Odpowiada to równości

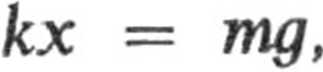
co jest identyczne z warunkie Druga pochodna

II

równowagi sił.

d²E_p

dx²

— k > 0,

mg

k

a minimum, co odpowiada warunkowi

zatem funkcja E_p w punkcie x równowagi trwałej.

2.45. Amplituda ruchu

x² +

V

4tcv

6,0 - 10

-2

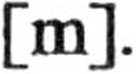
Faza początkowa ruchu określona jest wzorei

tga = -

v

2nvx

- 0,64,

2.46. Początek układu współrzędnych umieszczamy w środku Ziemi. Siła działająca na kulkę ma postać

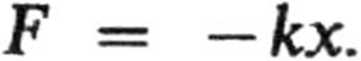
Na powierzchni Zie

II

i siła ta równa się ciężarowi kulki, a więc

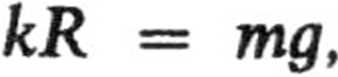
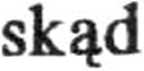
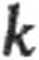
mg R ‘