Mechanika ogolna0088

()slalcc/,nic równinne I ,n griu igc'n opisiijnce zjawisko melin nklmlil będzie* na s(t*puj ące:

2

y— (Pj +2-P₂ + 8-P₃)cp_I = M-2-P₃ -^(sina + p-cosa),

czyli przyspieszenie kątowe bryły 1 układu wynosi:

•2g.

^lPi

M-2-P, -T] (sina + p- cos a)

(P₁+2P₂+8-P₃)r₁²

Przykład 32

Mamy układ mechaniczny złożony z krążka i wodzika połączonych ze sobą sprężyną o sztywności k. Krążek porusza się ruchem płaskim po chropowatej i odkształcalnej sprężyście powierzchni poziomej. Na wodzik działa siła zewnętrzna G (rys. 107). Opisać zjawisko ruchu, wykorzystując równania La-grange’a, przy założeniu, że masy obu brył są znane.

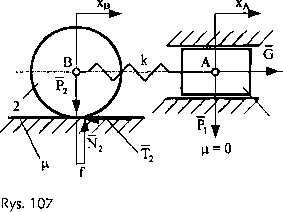
Dane:

G [N],

p )

¹ | - siły ciężkości działające na krążek i wodzik [N],

r - promień krążka [m],

1 p - współczynnik tarcia suchego krążka, f- współczynnik tarcia toczenia krążka [m].

Krążek może się przemieszczać niezależnie od ruchu wodzika, układ posiada więc dwa stopnie swobody. Za współrzędne uogólnione układu przyjmiemy odpowiednio przemieszczenia punktów A i B brył:

qi=x_A-

^2 ~ ^XB ’

prędkości uogólnione wynoszą:

qi=^xA>

^2 ~ ^XB'

Określmy zależności kinematyczne. Krążek jest w melin płaskim, tuk więc:

Dostaniemy energię kinetyczną układu:

E = E^ + E^ =— m, -x* +—m, -x_B +—I_B - co?.

₂ i a ₂ ² B 2

Moment bezwładności krążka wynosi:

I_B = — m₂ • r² = -^-r².

^B 2    ²    2-g

Uwzględniając powyższe zależności kinematyczne, mamy:

Energia kinetyczna jest funkcją dwóch prędkości uogólnionych. Korzystając z przykładu 29 (rys. 104), określimy siły uogólnione układu:

Q₁=G-k(x_A-x_B^

Q₂=-k(x_B-x_A)-^p^.

Wyznaczmy teraz poszczególne składowe równań Lagrange’a:

= 0,

SE

Sx.

dE

Sx_n

= 0,

SE P, . Sx “ g^X/

SE _ 3 P₂ . Sx_B 2 g ^X®’

dt^Sx_AJ g ^A’ dt

J

3 P₂ ..

—x,

2 g

Podstawiając do równań Lagrange’a, będziemy mieli:

^pi ••

= G-k(>