Mechanika ogolna0088

()sliilec/,inc równanie I ,np,riingc'n opisiijncc zjawisko melin ukliulil będzie* na-Niknij ii.ec:
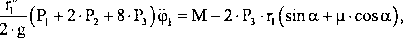
czyli przyspieszenie kątowe bryły 1 układu wynosi:
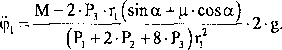
Przykład 32
Mamy układ mechaniczny złożony z krążka i wodzika połączonych ze sobą sprężyną o sztywności k. Krążek porusza się ruchem płaskim po chropowatej i odkształcalnej sprężyście powierzchni poziomej. Na wodzik działa siła zewnętrzna G (rys. 107). Opisać zjawisko ruchu, wykorzystując równania La-grange’a, przy założeniu, że masy obu brył są znane.
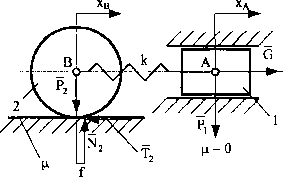
Dane:
G [N],
Rys. 107

dzik [N],
r - promień krążka [m], p - współczynnik tarcia suchego krążka, f- współczynnik tarcia toczenia krążka [m].
Krążek może się przemieszczać niezależnie od ruchu wodzika, układ posiada więc dwa stopnie swobody. Za współrzędne uogólnione układu przyjmiemy odpowiednio przemieszczenia punktów A i B brył:
=xA.
O2 ~ XB>
prędkości uogólnione wynoszą:
0i =*A.
Ó2 = *B-
Określmy zależności kinematyczne. Krążek jest w ruclm płaskim, tak więc:
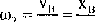
r
r
Dostaniemy energię kinetyczną układu:
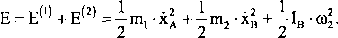
Moment bezwładności krążka wynosi:
IB=-m2-r2=-Ł.r2.
B 2 2 2-g
Uwzględniając powyższe zależności kinematyczne, mamy:
E-^-x2+|^-x2 =E(xa,xb).
Energia kinetyczna jest funkcją dwóch prędkości uogólnionych. Korzystając z przykładu 29 (rys. 104), określimy siły uogólnione układu:
Qi =G~k(xA-xB^
Q2 =-k(xB-xA)-P^.
Wyznaczmy teraz poszczególne składowe równań Lagrange’a:
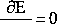
óxA ’
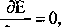
_SE_=:ą. dE _ 3 p2 -9xa 8 XA’ 2*b 2 8 X
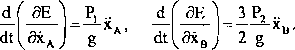
Podstawiając do równań Lagrange’a, będziemy mieli:
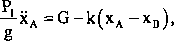
Wyszukiwarka
Podobne podstrony:
Mechanika ogolna0088 ()slalcc/,nic równinne I ,n griu igc n opisiijnce zjawisko melin nklmlil będzie
Mechanika ogolna0061 122 Płaszczyzna xy jest tzw. płaszczyzną porównawczą. Zakładamy, że potencjał n
Mechanika ogólna0061 122 Płaszczyzna xy jest tzw. płaszczyzną porównawczą. Zakładamy, że potencjał n
Mechanika ogólna0061 122 Płaszczyzna xy jest tzw. płaszczyzną porównawczą. Zakładamy, że potencjał n
mechanika ogolna�3 Zadanie 6 Wyznaczyć siły w prętach przegubowych O A i OB., tworzących wspornik AO
Mechanika ogolna0005 10 Równanie wektorowe opisujące ruch punktu materialnego ma postać wynikającą z
Mechanika ogolna0008 16 Z równania (23) mamy: N = P • cos a Siła tarcia rozwiniętego wynosi odpowied
Mechanika ogolna0013 20 W układzie nieruchomym równanie opisujące ruch punktu materialnego zapisywal
Mechanika ogolna0015 30 Ruch występuje tylko na kierunku osi x,. Równanie drugie i trzecie są równan
Mechanika ogolna0019 38 Równania (79) to rzuty wektora pędu środka masy na poszczególne osie układu
Mechanika ogolna0020 40 Są to różniczkowe równania ruchu środka masy układu, czyli dynamiczne równan
Mechanika ogolna0025 50 z x układ punktów materialnych, np. żyroskop Rys. 232.7. Geometria mas2.7.1.
Mechanika ogolna0029 58 (116)m-*S=XPix i=lm-ys=ŻPiy i=l m‘Zs = ŻPiZ i=l Są to różniczkowe równania r
Mechanika ogolna0039 78 _ nK0=S^xmi Vi’ i=l po zrzutowaniu tego równania na układ odniesienia dostan
Mechanika ogolna0046 M S;
Mechanika ogolna0089 Powyższe równanie zapisujemy w postaci: Jest to układ dwóch równań różniczkowyc
więcej podobnych podstron