mech2 106

211

210

^b2= -|^aa⁼ T^ai ^siDa-

2G

Z równania równowagi sił dla płytki otrzymamy

E ^ = -N₂ + B₂ = O,

2G

= B₀ = —- a- sina .

a *

2 ~ "2

Z równania równowagi dla klina

EY_i = G cos a - N₂ sin a -    = O,

G cosa - ~ sin²a - -^r a^ = O,

^a-i =    6

cosa

2 sin a + 1

W zadaniu oc = 30 i stąd

=

V3 '

2 yj

£_0rZyatamy z równań równowagi

2X_i = 2T₂ - B = O,

ZY_i = 2N_n + 2N₂ - Q = O,

EM₀ = Q(d -b) - 2N₂ć + Bo = 0.

z CD

Ostawiając do (3) otrzymamy

2T₂ = B ^N2 ⁼ ^ 2g

f (d-b)

^a * S 5'" -ćf *

CD

(2)

(3)

Zadanie 5

Obliczyć na jakiej najkrótszej drodze może zahamować samochód z poprzedniego zadania, jadąoy z prędkością v₀, jeżeli hamują tylko tylne Icoła. Znaleźć reakcje działające na koła podczas hamowania.

(d + cf)

Odp.

s -

2gf(d - b)" ’

„ b + cf

^N1 = ^Q 2(d + cTJ ’

d-b

^N2 = ^Q 2(d + cTJ •

Zadanie 4 (rys. 143)

Obliczyć z jakim maksymalnym przyspieszeniem może ruszać samochód

~    ’----*---">--¹--1-    - - — ~ T J -JT--______J_C_J

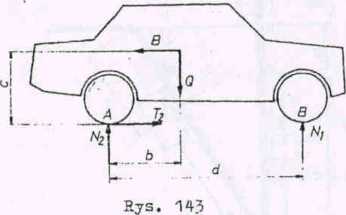
Rozwiązanie

Podczas ruszania tylne koło jest napędzane w kierunku przeciwnym do trygonometrycznego, co powoduje powstanie siły taraia gruntu o zwrocie zgodnym z ruchem samochodu. Gdy założymy ruszanie z maksymalnym przyspieszeniem, siła taraia T₂ = f Ng. Przednie koła nie są napędzane i poruszają się bez oporów, więo = O. Do środka ciężkości samochodu przykładamy

fikcyjną siłę bezwładności

- R.

^B = t‘'

i *

■-Ł

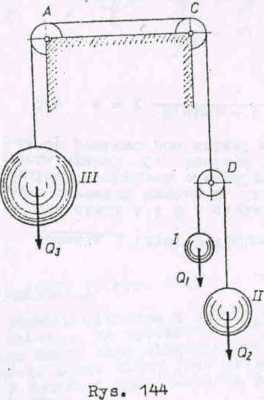
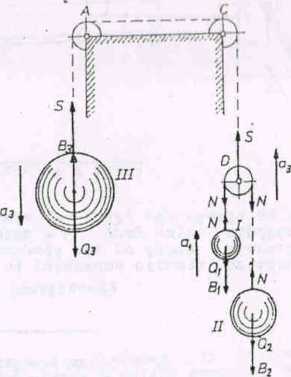
C;

Rys. 144a