s118 119

118

3.3. Macierz odwrotna

1. Wyznaczyć macierz		odwrotną macierzy
	"1	2 -3'
A =	2	-1 4	•
>	3	1 -1

Rozwiązanie

Przypomnijmy, że macierz odwrotna A~^l do macierzy kwadratowej A istnieje jedynie wtedy, gdy macierz A jest nieosobliwa, tzn. gdy det(A) ^ 0. Dla dowolnej macierzy nieosobliwej istnieje dokładnie jedna macierz odwrotna. Algorytm wyznaczenia macierzy odwrotnej zawiera cztery punkty:

i.

• • n.

• • • m.

iv.

obliczyć det(A),

utworzyć macierz transponowaną A¹,

utworzyć macierz dołączoną A^l}, czyli macierz dopełnień algebraicznych,

A"¹ -

det(.4)

A

u

Korzystając z tego algorytmu, wyznaczym}' macierz odwrotną macierzy A. Ponieważ:

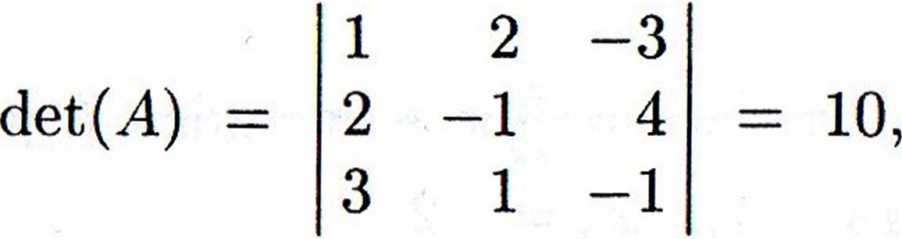
więc macierz A jest macierzą nieosobliwą, zatem istnieje macierz odwrotna A ¹ Transponując macierz A mamy

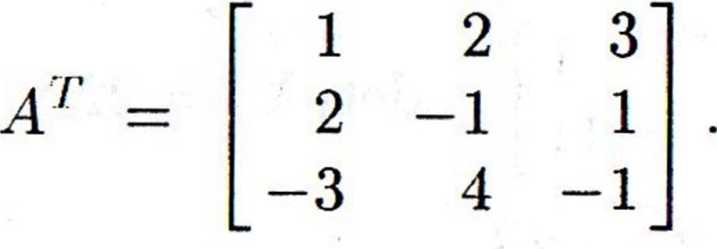
Szukamy macierzy dołączonej A^l\

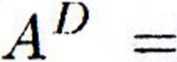
Au	A12	A13
A21	A 22	A 23
A$i	A32	A33

Au — (—1)

1+1

-1 1

4    -1

3, Ai2 — ( —1)

1 + 2

A-21 — ( —1)

2+1

A31 — ( —1)

3+1

2 3 4 -1

2 3 -1 1

= 14

= 5

A-22 — (“ 1)

-4-32 — (~1)

2+2

3+2

2 1

3 -1

1 3 3 -1

1    3

2    1

■4-13 — ("1)

1+3

4-23 — (~1)

2+3

4-33 — ( —1)

3+3

2 --3

1 2

-3 4

1 2 2 -1

1

4

5,

- -10

= -5

a więc

-3 -1	5
14 8	-10
5 5	-5 mm
° przez det(A)
3 1	5
10 10	10
14 8 10 10	-1
5 5	5
10 10	10

A" -

Dzielimy każdy element macierzy A° przez det(A) i otrzymujemy

4-¹ -

Dla sprawdzenia rachunków obliczamy iloczyn

4-A^-1 -

1	0	0
0	H	0
0	0	1

co oznacza, że macierz odwrotna jest poprawnie wyznaczona.

2. Dla jakich wartości parametru k, macierz

A =

k	1	2 k
1	0	-1
3	H	0

jest macierzą nieosobliwą ?