skan0296

Elektrochemia 299

pH = pK_a + lg

soli

Dc

(9)

Obliczona stąd przybliżona wartość pH wynosi 4,756.

c) Stałą dysocjacji amoniaku NH₄OH NH₄ + OH^- wyraża równanie

(10)

^oh- _ ^coh- }'± "nh₄oh (c_z - c_OH-) c® ’

gdzie c._Ł jest stężeniem początkowym NH₄OH, a współczynnik aktywności nie-zdysocjowanej zasady przyjęto za równy 1. Amoniak jest słabo zdysocjowany i, podobnie jak w punkcie a), nietrudno wyprowadzić przybliżone wyrażenie

^aon~ =

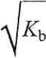
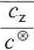
skąd można obliczyć przybliżoną wartość pH:

pH= p£_w-— p/ć_b-lg

c.

= 13,997— • (4,75 - lg 0,1) = 11,123.

Dokładną wartość pH otrzymamy, przekształcając równanie (10):

^y± ⁺ K_b^c®x- K^c_zc® = 0,    (11)

gdzie * oznacza stężenie jonów' OH^-. Identycznie jak w punkcie a) znajdujemy x i y± - zob. tab. 6.13.

Tabela 6.13

i	/[M]	logy±	y±	A		*; [M]		pH
0			i	7,113 •	10^-6	1,325	10^-3	11,119
1	1,325 • 10^-3	-0,01853	0,958	6,532 •	10^-6	1,382	10^-3	11,119
2	1,382- 10^-3	-0,01893	0,957	6520 •	10"^6	1,383	10^-3	11,119
3	1,383 • 10^-3	-0,01893	0,957	6,519 •	10^-6	1,383	10^-3	11,119

Dokładna wartość pH 0,1-molowego roztworu amoniaku w 25°C nieznacznie odbiega od wartości przybliżonej

2

x y±

pH = pAT_w + lg -#= 13,997 + lg

1,383 -10^-3- 0,957

,119,

toteż dla słabych zasad metoda przybliżona jest w' zupełności wystarczająca.

d) Analogicznie jak w punkcie b), można z równania (10) wyprowadzić wyrażenie