006

10

Często sygnały NMR są znacznie szersze, niż to wynika z wartości czasu 7j. Spowodowane jest to jeszcze jednym rodzajem relaksacji. Spełnienie warunku rezonansu powoduje powstanie magnetyzacji M _lt której wektor obraca się względem pola B₀ z częstością w (rys. 1,4.2). Po przejściu przez warunek rezonansu dochodzi do wymiany energii pomiędzy poszczególnymi jądrami tak, że ich całkowita energia potencjalna w polu B₀ nie ulega zmianie. Objawia się to zróżnicowaniem częstości, z jaką obracają się poszczególne wektory ji_tL (rys. 1.4,2), czyli zanikiem magnetyzacji M_L.

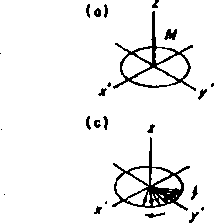
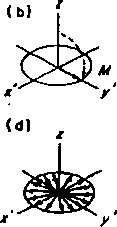
Rys. 1.4.2. Zachowanie się magnetyzacji w płaszczyźnie (xy). (a) Wektor magnetyzacji w star nie równowagi; (b) bezpośrednio po rezonansie wektor magnetyzacji wiruje, razem z osiami a* i /, z częstością rezonansową; (c) zróżnicowanie częstotliwości precesji poszczególnych jąder; (d) zanik magnetyzacji w płaszczyźnie (jcy)

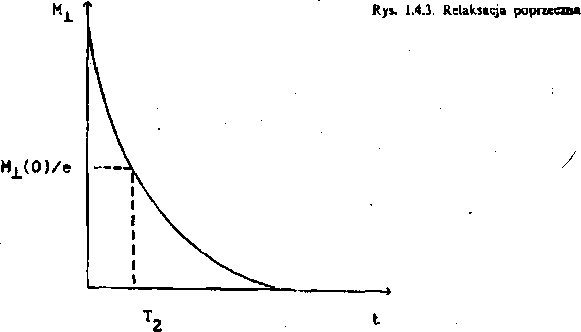
Proces taki nazywa się relaksacją spin-spin i jest charakteryzowany stałą czasową T₂ nazywaną czasem relaksacji spin-spin;

dMJdt-    (1.4.6)

lub po scałkowaniu

AM0)e-"^r’.    (M.7)

Proces ten przedstawia rys. 1.4.3.

Zwykle pole magnetyczne B₀ nie jest jednorodne, co dodatkowo przyspiesza proces rozchodzenia się wektorów (rys. 1.4.2). Dlatego rzeczywisty czas relaksacji (T?), nazywany czasem relaksacji poprzecznej, jest krótszy od czasu relaksacji spin-spin (T₂). Ponadto, relaksacja składowej A/_i magnetyzacji nie może zachodzić wolniej niż składowej M_t. Stąd nierówność:

7? T₂ < 7].    (1.4.8)

Rzeczywisty czas życia jądra w określonym stanie wyznacza więc Tf (w idealnie jednorodnym polu magnetycznym TJ i szerokość połówkowa sygnału NMR wyraża się zależnością

(1-4.9)

t.5. Ekranowanie jądrowe

Przy omawianiu zjawiska rezonansu magnetycznego uwzględniano tylko przykładane z zewnątrz pola magnetyczne. Tymczasem na jądra działają również pola magnetyczne pochodzące od elektronów danej molekuły, jak również od elektronów sąsiednich cząsteczek. Na przykład dla trzech grup równocennych protonów w molekule etanolu istnieją trzy rodzaje pól lokalnych:

HO—CHj—CHj

R)ok Bu, k    B?ok

i rezonans zachodzi w trzech różnych częstościach:

vŁ = y_p(5₀ + flU)/2n_f    ' (1.5.1)

gdzie y_p jest współczynnikiem magnetogirycznym protonu. Powierzchnie pod sygnałami są proporcjonalne do liczby protonów w poszczególnych grupach i mają się do siebie jak 1:2:3.

Pola lokalne zawarte w równaniu (1.5.1) oznaczają średnie wartości pól dla wszystkich, podlegających uć.ednieniu, stanów wewnątrz- i międzymolekular-nych. Do powstania tych pól konieczne jest zewnętrzne pole magnetyczne E₀, które wymusza ruchy (prądy) elektronów. Spełniona jest przy tym relacja:

(1.5 Ja) lub

Ąi, =    (1.5.2b)

gdzie a, zależy tylko od fizykochemicznych własności badanego układu i jest nazywana stałą ekranowania. Jest to tensor (równanie (1.5.2a)}, który dla cieczy i gazów redukuje się do postaci współczynnika liczbowego z powodu szybkich, uśredniających ruchów drobin (równanie (t.5.2b)).

:41