11 (12)

Biblioteczka Opracowań Matematycznych

70/

\~ ^J Cl

xdx

sin^: x

71/

rcos

J cii

= -x ctgx+ jctgxdx= —xctgx+ Injsin a| + C

u = x du = dx , dx

dv = —— v = -ctgx sin" x

r a cos adx	U = X	du =	dx
---= ^J sin ^3 a	, cos dx = . , sin a	V=J	d\’

= /

Pomocniczo obliczamy:

rcos xdx _ sin a = /

sin ' x cos xdx = dr 1

rdt    r __3j    -1

=    -r-=    /    £* = -5- = -

³ I’    ³    It¹

1

2 sin ² x

,    x i r dx

¹ ~ ^_ o    :— ⁺ T It^-;— - ~

2 sin x 2 ^J sin x

2 sin * x 2

--ctgx + C

72/

Jarccos xdx -

u = arccos x du =

-dx

dv = dx

•y/TTi

= x arccos a +

= x arccos .t +

1 -x² =l²

73/ r ₂ ,

-Jarccos xdx =

= a arccos x

v = x rtdt

xdx

- 2xdx = 2 rdt

u = arccos x

- f— = xarccosx--J\-x² +C ^J r

-dx

du =

dv = arccos xdx v = x arccos a- - V 1-a²

= Aarccoś a - y/l-A² arccoa

74i

x

-M

•Aarccoarr/r

• =AarccoSA

arccosr-2A+C

. x arcsm-

^dx =

u = arcsim- c/m = 2

-(fi

i

dv = —^L= v= \ch~-2-l2-x v2-a ³

Pomocniczo obliczymy całkę:

V2-j

2,1

= -2il2-x arcsin— + f-^~ ■ ^A dx 2 ³

^1_T

f    dx=2\ L- - ^x dx=2\~^= =

2+x=z² dx=lzdz

= 4jdt=4V2+^+C

^JV(2-xX2+x)

v~r*

arcsin —

f——i-dx = 4^2 +x - 2y/2-x arcsin —+ C

75/

du=dx

U=X

Jxsinrcosrgfcr=-|2xsitucosr^y=- J.tsin2x<£=-^    ^ _-cos2r =-^cos2r+

+ — \cos2xdx = -—cos2x + -sin 2x + C

4 J    4    8

76/

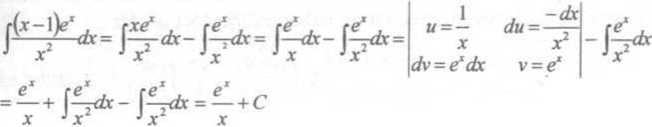
4. Całki funkcji wymiernych

Jeżeli wyrażenie podcałkowe ma postać funkcji wymiernej to mamy do czynienia z całkowaniem funkcji wymiernej. W zależności od postaci tej funkcji możemy stosować różne metody całkowania. Mogą wystąpić zatem przypadki:

a/ ułamek podcałkowy jest właściwy (tzn. mianownik ma wyższy stopień niż licznik), wówczas rozkładamy mianownik na czynniki a cały ułamek rozkładamy na sumę ułamków prostych pierwszego lub drugiego rodzaju - metoda współczynników nieoznaczonych.

Funkcję wymiemąjednej zmiennej postaci:

-21-