12 (11)

Biblioteczka Opracowań Matematycznych

A

(1.24)    (_v _ _ay nazywamy ułamkiem prostym pierwszego rodzaju.

Funkcję wymiemąjednej zmiennej postaci:

Ax + B

(1.25)    (_v:₊£_v+ J nazywamy ułamkiem prostym drugiego rodzaju.

b/ ułamek podcałkowy jest niewłaściwy, wówczas należy wyłączyć wyraże--nie całkowite poprzez wykonanie dzielenia wielomianów. Resztę z tego dzielenia należy zapisać w postaci ułamka właściwego i postąpić jw. cJ licznik ułamka podcałkowego jest pochodną mianownika tego ułamka. Należy wówczas zastosować wzór (1.22) ze str. 14.

d1 licznik ułamka podcałkowego można rozłożyć na składniki, z których jeden jest pochodną mianownika a drugi stanowi nowy przypadek, e/ funkcję wymierną przez odpowiednie podstawienie da się sprowadzić do postaci funkcji wymiernej, której całka jest postaci arctgx.

r dx x-k=4bt _ r yfbdt _ -Jb r dr l

^(x-kf+b dx-4bdt 'br+b b •'/*+! -Jb

= —j= arcigl + C =

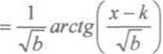
PRZYKŁADY CAŁKOWANIA

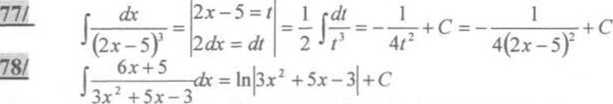
79/

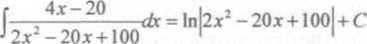
80/ r 6+s

hix+x¹

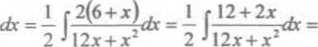
|ln|l2x + x²| + C

x + 2

81/	r ^A	r ^A _	x + 2 = t
	^J x^2 +4x + 4	(x + 2)^2	ll ■s
82/
	(• dr	f	dx
	^J-x^2 +6x-	5 ^J(x-	-sX*-D

r

■"r² t

• + C

Pomocniczo rozkładamy funkcję wymierną na ułamki proste. A zatem: 1    A B /4(x-l)+5(x-5) x(A + B)-A-5B

(x-5X*-l) jc —5 x -1    (x-5X*~l)    (x — 5X^jc ^— 0

.4+5 = 0

Stąd:    1-/1-55 = I

A = -4

I

B =--

4

/ = --    + i f— = ---ln|x-5| + -ln|x-l| + C

4^Jx-5 4 ^ jc — 1    4 ^1    1 4 ^1    1

1 r dx 1 r dx

83/    f —_= f.

³ 4x - 5x^{2 J}

dx

= 1

’ x(4 - 5x)

_1_ A_ B x(B-SA)+4A

x(4-5x) x 4-5x    x(4-5x)

5-5.4 = 0 4/4 = 1

A = — 4

5=* 4

/-i tŚL+Ł f ^A _^lnH ^lnl⁴~⁵-^yl, _r

4 x 4 M-5x 4    4

⁸⁴⁷    t .u"

r^U - r*T—**,³ f-jiiU+ 11 f-^L-,

^Jx²-x-2 ^J x²-x-2    2^Jx²-x-2    2 ^Jx²-x-2

= ^-ln|x²-x-2|+t    t-= ^-ln|x²-x-2|

2    ^1    1    2 ^J ( I y 9    2    '    '3

r"!; ~4

tli

+ 0

-23-