42308 Untitled Scanned 62 (2)

GEOMETRIA ANALITYCZNA 65

TRAPEZY

429. Czworokąt ARCD pokazany jest na rysunku.

a) Uzasadnij, żc czworokąt ABC U jest trapezem.

b) Znajdź równania prostych zawierających prze-

kątne tego czworokąta, c) Oblicz pole czworokąta ABCD.

430. Dane są punkty A = (1, 1). B = (9. 5), C= (5, 8). Wyznacz współrzędne punktu D wiedząc, żc czworokąt AHCDjcsi trapezem prostokątnym, którego kąt przy wierzchołku A jest prosty.

431. Punkty Ą = (I, -2). D = (-2. 2) są kolejnymi wierzchołkami trapezu ABCD. Prostą .v + 2y -7 = 0 jest osią symetrii tego trapezu. Znajdź pozostałe wierzchołki trapezu.

432. Punkty A = (0. -5), B - (4. 3) i C= (-1, 3) są wierzchołkami trapezu równoramiennego ABCD o podstawach AB i CD. Wyznacz wierzchołek D i oblicz pole trapezu.

433. R Odcinek o końcach A = (3, 3) i B = (0,0) jest podstawą trapezu ABCD. Druga podstawa trapezu jest cztery razy dłuższa i ma środek w punkcie K = (3, -1). Wyznacz współrzędne wierzchołków C i D tego trapezu oraz oblicz jego pole.

RÓWNANIA. NIERÓWNOŚCI. UKŁADY RÓWNAŃ I NIERÓWNOŚCI

nierówności i układy nierówności liniowych z dwiema niewiadomymi

434. Punkty A =(-100, -300) i /? = (7, 19) są końcami odcinka AB. Sprawdzimy, czy odcinek AB ma punkt wspólny z prostą o równaniu y=3.v - 1.

• Współrzędne punktu A spełniają nierówność y >3jy- I. gdyż -300 > 3*(—100) - 1, natomiast współrzędne punktu B spełniają nierówność y < 3.v- 1 (19 < 3-7 - 1).

• Zatem punkty ,4 i B należą do różnych półpłaszczyzn wyznaczonych przez prostą y = 3.v- 1, a to oznacza, że odcinek AB ma punkt wspólny z prostą o równaniu y=3.v- 1.

Sprawdź, czy odcinek, którego końcami są punkty K = (80. 402) i /. = (-30, -148), ma punkt wspólny /. prostą o równaniu 5x - y + 3 = 0.

435. Dane są zbiory A = {(.w y): a - 2y > 0 a xe R a ye R } i B={{x,y): y>0,5.t-2 a as K a ye R }. Zaznacz w układzie współrzędnych zbiór

a) AnH:

b) AuB-

c) A\H.

436. Zbiór A jest zbiorem punktów, których współrzędne spełniają układ nierówności

tego

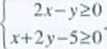
a) Naszkicuj w układzie współrzędnych zbiór A.

b) Oblicz długość odcinka, który jest częścią wspólną zbioru A i prostej o równaniu 4x + 3y- 20 = 0.