59352 img478 (2)

Niech P(x, y) będzie poszukiwanym punktem. Ponieważ należy on do paraboli y = x², więc P(x, x²). Oznaczmy odległość punktów P i 4 przez d. Mamy

d(x) = ]j(x - O)² + (x² - 1 )² , czyli d(x) = ]jx⁴ - x² + 1 .

Należałoby wyznaczyć najmniejszą wartość tej funkcji. Ma ona jednak znów skomplikowaną do różniczkowania postać. Podobnie jak w poprzednim przykładzie, tak i tu wyznaczymy najmniejszą wartość funkcji (uzasadnij, dlaczego możemy tak postąpić):

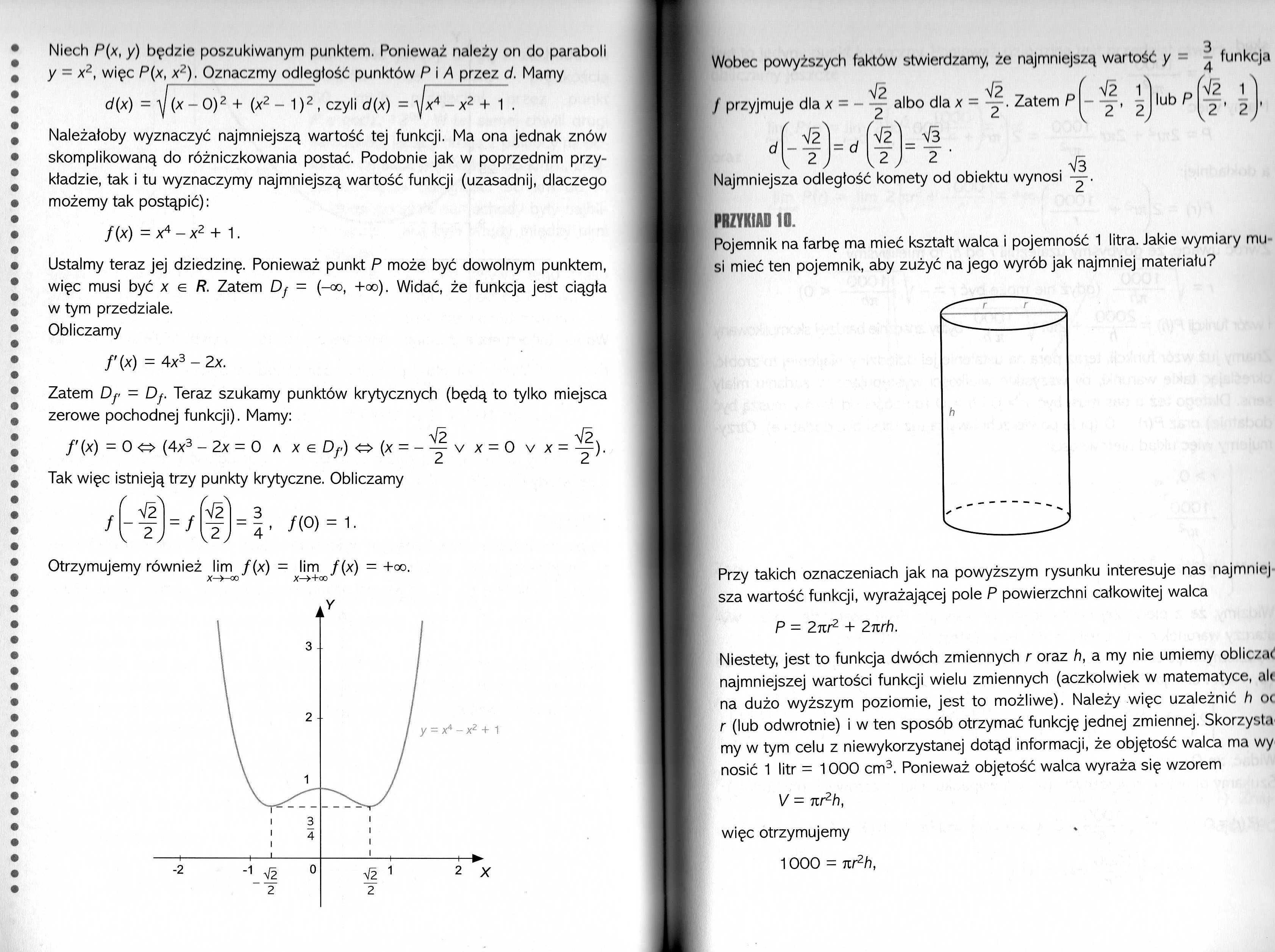
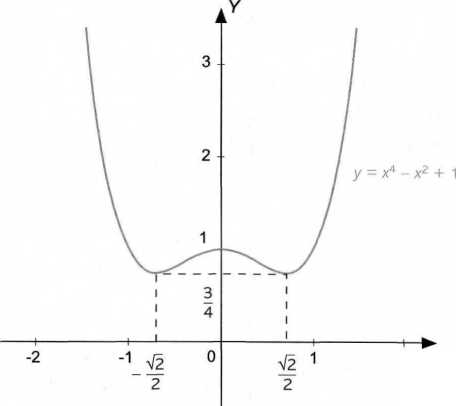
f(x) - X⁴ -x² + 1.

Ustalmy teraz jej dziedzinę. Ponieważ punkt P może być dowolnym punktem, więc musi być x e R. Zatem Dy = (-co, +oo). Widać, że funkcja jest ciągła w tym przedziale.

Obliczamy

f'(x) = 4x³ - Zx.

Zatem Dy- = Dy. Teraz szukamy punktów krytycznych (będą to tylko miejsca zerowe pochodnej funkcji). Mamy:

f'(x) = 0 <=> (4x³ - 2x = 0 a x e Dy-) <=>(x = -^=v x = O

v

Tak więc istnieją trzy punkty krytyczne. Obliczamy

4-f

= /

f =7- /(«) = '■

Otrzymujemy również lim /(x) = lim /(x) = +oo.

X—^—00    X—>+00

2 X

Wobec powyższych faktów stwierdzamy, że najmniejszą wartość y = funkcja

f przyjmuje dla x = - — albo dla x = Zatem P

V2	= d	(rz)
l 2j		UJ

2

Najmniejsza odległość komety od obiektu wynosi

-f, ^ Mub P

. V3

^2

2 '

1

2

PRZYWAB 10.

Pojemnik na farbę ma mieć kształt walca i pojemność 1 litra. Jakie wymiary mu si mieć ten pojemnik, aby zużyć na jego wyrób jak najmniej materiału?

Przy takich oznaczeniach jak na powyższym rysunku interesuje nas najmniej sza wartość funkcji, wyrażającej pole P powierzchni całkowitej walca

P = 2tir² + 2nrh.

Niestety, jest to funkcja dwóch zmiennych r oraz h, a my nie umiemy obliczać najmniejszej wartości funkcji wielu zmiennych (aczkolwiek w matematyce, alt na dużo wyższym poziomie, jest to możliwe). Należy więc uzależnić h oc r (lub odwrotnie) i w ten sposób otrzymać funkcję jednej zmiennej. Skorzysta my w tym celu z niewykorzystanej dotąd informacji, że objętość walca ma wy nosić 1 litr = 1000 cm³. Ponieważ objętość walca wyraża się wzorem

V —

więc otrzymujemy

1000 = nr^zh,