63553 MATEMATYKA053

98 ID Rachunek nUnfcgkowy

Rysunki l.l i 1.2 stanowią ilustrację do definicji Heinego i Cauchy'ego granicy funkcji.

A teraz sformułujemy definicje granicy niewłaściwej w punkcie x₀:

x₀)=>(lim f(x„) = +oo))

DEFINICJA HEINEGO (lim f(x)-+oc) oA((x, fcS(x„).n c N a limx

DEFINICJA CAUCHY EGO.

(lim f(x) - 400) oAVA(0<|x-xJ<fi=> f(x)> M).

x >*₀    M 6 -0 x

Sfoimulowanie definicji granicy niewłaściwej -x funkcji f w punkcie x₀ pozostawiamy Czytelnikowi. Na rysunkach 1.3 i 1.4 przedstawiono wykresy funkcji, które mają w punkcie x_n granice niewłaściwe.

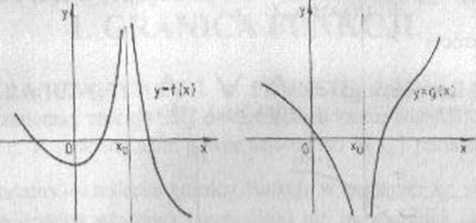
lim fix)»

X *x„

lim g(x)« •» * *x„

Rys 14

Rys 1 3

PRZYKŁAD 1.1 Korzystając z definicji I łcincgo granicy

funkcji obliczymy

•~3x    —3 x

a) lim-1, b) lim --—r

*-*2 (x + I)‘    *-* ¹ (x 4 I)*

a) Rozpatrywana funkcja f jest określona dla xr-D ł(-oo,-1)u(-1,+oo).

Niech (x_n) oznacza d o w o I n y ciąg taki. że

x_n f= S(2)c D, n eN oraz limx_n=2.

a-»t)

Obliczamy granicę ciągu (f(x_n)) korzystając z poznanych wcześniej twierdzeń o granicach ciągów:

Zatem

lim f(x) = lim

*-*2    »-*(x+l)²

b) Niech (x_n) będzie dowolnym ciągiem takim, źc x_n €S( 1), neN oraz limx_n=-l,

Ponieważ

lim f(x_n) = lim

n-*tc>    n »no( x

iJlL

«.+«* 10 + J

+00.

więc

= +00.

lim f(x) = lim ~^3x, x_-l    (x + I)'

PRZYKŁAD 1.2 Na rysunku 1.5 przedstawiono wykres

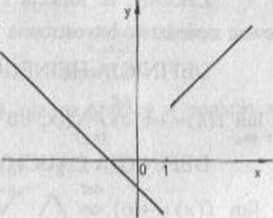
funkcji f(x)= ’^C—1 x*l.

|x-l|

Zauważmy, że

1)    dla każdego ciągu (x_n) takiego, ze x_n > I,n g N i x„ > I za-chodzi warunek f(x_n) —> 2;

2)    dla każdego ciągu (x_n) takiego,

że x_n < l.n c N i x„ —> I za-chodzi warunek f (x _n) -+ -2.    Rys 1.5

Ponieważ dla różnych ciągów (x_n) zbieżnych do I ciągi (f(x_n)) mają różne granice, więc granica funkcji f w punkcie x₀ = 1 nie istnieje. ■

W powyższym przykładzie można mówić o granicach jednostronnych funkcja f ma w punkcie x₀ = 1 granicę lewostronną równą -2 oraz ma granicę prawostronną równą 2, co zapisujemy:

lim f(x)- 2

x-»l-

lim f(x) = -2,

x-*l-