65012 str045 (5)

S 6. CAŁKA FUNKCJI ZMIENNEJ ZESPOLONEJ 45

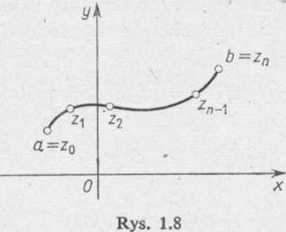
Na każdym łuku częściowym z_k__xz_k obierzmy dowolny punkt = £_k+ir}_k i wprowadzając oznaczenia

(6.2)    z*-z_k_, = Az_k, k = 1,2.....n,

utwórzmy sumę

(6.3)    S„ =f(C_l)Az_l+f(t₂)Az₂ + ...+K_H)Az_n = £/(«/Iz*.

k—1

Jeżeli istnieje granica skończona ciągu sum (6.3) przy założeniu, że ilość łuków częściowych dąży do nieskończoności, a ich długości do zera i jeżeli granica ta nie zależy od sposobu podziału krzywej C na łuki częściowe i od wyboru punktów to granicę tę nazywamy całką krzywoliniową funkcji /(z) wzdłuż krzywej C i oznaczamy symbolem

(6.4)    if{z)dz.

c

Twierdzenie 1. Jeżeli funkcja f(z) = u(x, y)+iv(x^y) jest ciągła wzdłuż krzywej regularnej C, to całka (6.4) istnieje i daje się wyrazić następującym wzorem:

(6.5)    j'f(z)dz= f u(x, y)dx-v(x, y)dy+i $v(x, y)dx + u(x, y)dy.

cc    c

Korzystanie ze wzoru (6.5) przy obliczaniu całek funkcji zmiennej zespolonej wzdłuż krzywej C jest niewygodne. W zastosowaniach zamiast ze wzoru (6.5) korzystamy z następującego wzoru:

(6.6)    f/(z)dz= \f[z{tj]z\t)dt,

c    *

gdzie

z = z(/),

jest równaniem krzywej całkowania C.

Uwaga. Prawą stronę wzoru (6.6) otrzymujemy z prawej strony wzoru (6.5), stosując do całek krzywoliniowych, stojących po prawej stronie (6.5), twierdzenie o zamianie całki krzywoliniowej na zwykłą całkę oznaczoną.