00098499

286    l!t. FUNKCJE ZMIENNEJ ZESPOLONEJ

przy czym z uwagi na przyjęte założenia mamy A-o) f 0 oraz. A'(») * 0, więc

/l (a-) * U

Z równości (111 91) dostajemy

Arg.l'(*+) -• Arg/'(Zo)-*-ArgA'(» I)    01192)

Zauważmy, r; /godr.:ę i interpretacją geometryczną pochodnej fu ciec; i zespolone; zm:er.nci rzeczywiste; ipor p 3 tego rozdz.!. Arg* • * • i stanów: zb ór wszystkich traat łukowych kala skierowanego o wierzchołki. i.tir.icr.u początkowym ;S₀) zgodnie równoległym do Ox. oraz ramienia korcowym •'.S i /godnie równoległym do wektora jRe/.'(s - ).    )), stycznego w punkcie :_c do ł'^Jk'^J (W-W-

Ir.terpretac;a Arg.l'(i i i jot analogiczna i dotyczy kąta o wierzchołka w_a i ramionach: początkowym {T₀) i końcowym (T)—patrz rys. 111.19.

Równość (lii 92) wskazuje na to. źc na skutek odwzorowania w —/(z) o łożonych wyżej właściwościach kierunek styczny (.V) doznał obrotu (został odwzorowany na kierunek styczny ('/')). przy czym jedną z miar tego obrotu jest arg/'(r₀). Każda inna miara lego obrotu różni się od arg/'(;<,) ⁰ całkowitą wielokrotność 2n. Ponieważ liczba arg/"(z₀) i łuk (IH.8V) są od siebie niezależne. więc każdy kierunek (V) wyprowadzony z punku :₀ dozna na skutek odwzorowania w /(r) oblotu o kąt skierowany, którego jedną z miar ;cst argT(^r«)> a zatem kąt skierowany między dowolnymi dwoma takimi kierunkami me zmieni się (rys. 111.20) W szczególności zachowa sit

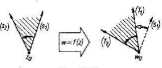
Rys. 111.20

prostopadłość kierunków. Jeżeli w obszarze I) znajdują się dwie rodzjny linii, ortogonalne jedna względem drugiej, to na skutek odwzorowania ohszaru D za pomocą funkcji holomorficznej i jednokrotnej przejdą one » dwie rodziny linii w obszarze O . które będą także ortogonalne jedna względem drugiej.

Def. Odwzorowanie konforemne obszaru D jest to oj w/u:; iwanie zachowujące kąt skierowany między każdymi dwoma kierunkami wyprowadzonym: z dowolnego punktu tego obszaru.

Udowodniliśmy zatem następujące twicrczeme.

Tw. Odwzorowanie obszaru O za pomocą funkcji holomorficznej i rótnowartoicio-wej Jest odwzorowaniem konforemnym tego obszaru.

Odwzorowania konforemne znajdują liczne zastosowania w zagadnieniach technicznych. Okazuje się na przykład, że obliczanie pewnych parametrów fizycznych ośrodka o złożonych kształtach, można za pomocą odwzorowań konforemnych sprowadzić do obliczenia tych parametrów dla kształtów mniej złożonych. Typowymi przykładami są tu obliczenia parametrów (np. pojemności) elektrycznych linii przesyłowych a złożonych przekrojach.

Uwaga. Omówiona tu konforemność odwzorowania za pomocą funkcji /(z) wyjaśnia interpretację geometryczną argumentu arg/'(z). W każdym punkcie i_a rozważanego obszaru arg/’(z₀) jest miarą łukową obrotu każdego kierunku wyprowadzonego z tego punktu, tj. obrotu, który nastąpi! na skutek odwzorowania w — /(;>.

W celu pełnej interpretacji geometrycznej pochodnej /'(z), zwrócimy jeszcze uwagę na moduł |/'(z)|. Ponieważ

Mtti-|/'{z₀)!Mz|'-ho(i/lrD

więc ;/'(*o)l jest granicą stosunku odległości |Jn»| punktów po przekształceniu do odległości |dz| punktów przed przekształceniem. Granica ta, zależna tylko od funkcji J\z) i punktu z₀, niezależna natomiast od sposobu w jaki Az -» 0, bywa nazywana współczynnikiem wydłużenia odwzorowania h>=/(z) w punkcie z₀. Jeżeli moduł |/fz| jest dostatecznie bliski zeru, to

1^! ~ l/'(*o)l \M

Trudności natury rachunkowej związane z odwzorowaniami, zmuszają nas niekiedy do posługiwania się tym przybliżeniem.

Dwa zagadnienia z zakresu odwzorowań konforemnych zasługują na szczególną uwagę.

Zagadnienie I. Dany jest obszar D i dany jest obszar D\ szukamy funkcji f(z) holomorficznej i jednokrotnej w obszarze D, która odwzorowuje go na obszar D‘.

Zagadnienie II. Dany jest obszar D i funkcja /(z) holomorficzna i jednokrotna w tym obszarze, szukamy obszaru D', na który funkcja /(z) odwzorowuje obszar D.

Pierwsze z tych zagadnień jest na ogół znacznie trudniejsze od drugiego. Efektywne znalezienie funkcji odwzorowującej dany obszar na inny dany obszar bywa bardzo trudne, a nawet praktycznie niemożliwe. Odnośnie zagadnienia I, ograniczymy się tu do podania ważnego twierdzenia, które dotyczy istnienia i jednoznaczności odwzorowania.

Tw. (Rikmanna, o odwzorowaniu). Jeżeli

1° D i D' są to obszary jednospójne, przy czym brzeg każdego 2 nich składa się co najmniej z dwóch punktów,

2° r₀ Jest dowolnym punktem w obszarze D, w₀ jest dowolnym punktem w obszarze D' oraz tp₀ jest dowolną liczbą z przedziału (—tr, +n),

to istnieje dokładnie jedna funkcja f(z) holomorficzna i jednokrotna w obszarze D, która odwzorowuje obszar D na obszar D' i taka, te

foa) = w₀ oraz    argf'(z₀) = rp₀