89043 MATEMATYKA042

76 li. Ciągi i szeregi liczbowe

Uwago l Ponieważ szeregi różniące się skończoną liczbą wyrazów są jedno cześnic zbieżne lub jednocześnie rozbieżne, więc twierdzenie pozostaje prawdziwe, gdy założeniu Oia_nt£ b_nspełnione jest nie dla wszystkich n e N,ale począwszy od pewnego n

•c    o

Uwaga 2 Jeżeli wyrazy szeregów £a„ i £b_n spełniają nierówność

n-l    rwl

«    *    «e

0<a„ Sb_n, neN . to szereg £a„ nazywamy minorantą szeregu £b_n, a szereg £b_n

n*l    tri    tul

nazywamy majorantą szeregu £a_n. Zatem kryterium porównawcze można sformułować

n-l

jak następuje;

(1)    Jeżeli dla danego szeregu o wyrazach meujcmnych istnieje major anta zbieżna, to szereg ten jest zbieżny

(2)    Jeżeli dla danego szeregu -o wyrazach nicujcmnyeli istnieje minoranta rozbieżna, to szereg ten jest rozbieżny.

KRYTERIUM CAUCHY'EGO (zbieżności i rozbieżności szeregów). Załóżmy, że dla szeregu £a_n o wyrazach nieujemnych istnieje skończona lub nieskończona granica

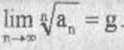
Wówczas:

(1)    Jeżeli g <l,lo szereg £a_n jest zbieżny.

(2)    Jeżeli g > 1, to szereg La,, jest rozbieżny.

Dowód (1). Ponieważ ciąg (^a^) ma granicę g, więc w

dowolnym otoczeniu liczby g znajdują się prawie wszystkie wyrazy tego ciągu Stąd wynika, że od pewnego n począwszy- wyrazy ciągu a_n) są mniejsze od dowolnie wybranej liczby pe(g,l). Istnieje więc taka liczba K, ze

0<^ < P< 1 dla n> K.

Stąd otrzymujemy

0£a_nSp^ft dla n>K.

Ponieważ szereg Lpⁿ jest zbieżny (geoni o ilorazie p€(0;l) ), więc z kryterium porównawczego wynika, że szereg £a_n jest również zbieżny.

■

77

2. Szeregi liczbowe

Dowód (2). Zakładamy teraz, że cłąg(^/a„) ma granicę g > 1. Stąd wynika, że prawie wszystkie wyrazy ciągu (^Ja_n ),a więc i ciągu

(aj, są większe od I. Zatem ciąg (aj nic może być zbieżny do 0. Szereg £a_n jest więc rozbieżny, gdyż nic spełnia warunku koniecznego zbieżności.    O

KRYTERIUM D AŁEM BERTA (zbieżności i rozbieżności szeregów). Załóżmy, że dla szeregu £a_n o wyrazach dodatnich istnieje skończona łub nieskończona granica

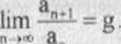
n

Wówczas:

(1) Jeżeli g< U to szereg £a_n jest zbieżny

(2) Jeżeli g>l, to szereg Xa_n jest rozbieżny.

U w u g a 1. Ostatnie dwa kryteria nic rozstrzygają, czy szereg jest zbieżny czy rozbieżny, gdy g = 1.

U w a g u 2. Jeśli na podstawie kryterium stwierdzamy, ze szereg o wyrazach nieujemnych jest zbieżny, to nie możemy nic powiedzieć o sumie tego szeregu poza stwierdzeniem, że ta suma jest skończona. Jeśli zaś stwierdzamy, że szereg o wyrazach nieujemnych jest rozbieżny, to jest on rozbieżny do + cc.

IJ w a g a 3 Sformułowane trzy kryteria zbieżności i rozbieżności szeregów możemy wykorzystać również do badania zbieżności szeregów o wyrazach ujemnych (nicdodaiiuch). Ponieważ szeregi £a_n oraz £(a„) są jednocześnie zbieżne lub jednocześnie rozbieżne, więc badanie zbieżności szeregu o wyrazach ujemnych możemy zastąpić badaniem zbieżności odpowiedniego szeregu o wyrazach dodatnich.

PRZYKŁADY BADANIA ZBIEŻNOŚCI I ROZBIEŻNOŚCI SZEREGÓW

PRZYKŁAD 2.4 Korzystając z kryterium porównawczego zbadamy zbieżność szeregów: