Image62 (9)

122

gdzie: r g

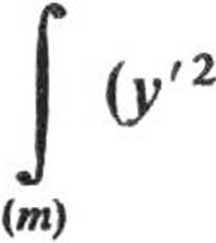
4- z'²) dm

(p g [O, 2tc], z g [O, h].

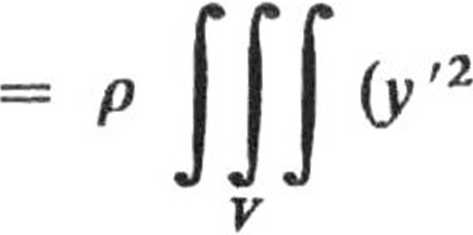
+ z'²) dx' dy' dz' =

2n h h

3 m nR²h

lii

0 0 0

sin²(p + z²) r dr d(p dz

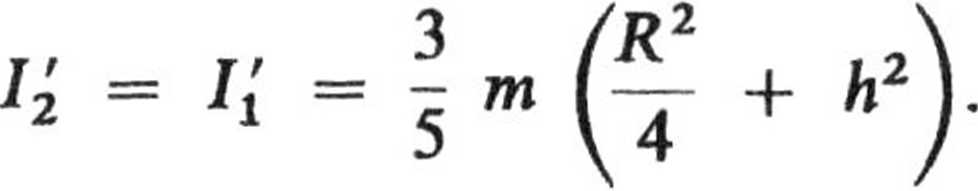
zR

2it h h

U =

(x’² + y^,z) dx' dy' dz' =

• 2

3 m

nR²h

r³ dr d(p dz

0 0 0

3

15

m R

3

Środek masy znajduje się na osi stożka, w odległości a = - h od wierzchołka Korzystając z twierdzenia Steinera ostatecznie dostajemy:

d. Środek masy pokrywa się z geometrycznym środkiem elipsoidy, a osie główne z jej osiami. Całkowanie po elipsoidzie można sprowadzić do całkowania po kuli jednostkowej, wprowadzając uogólnione współrzędne sferyczne:

x = a r cos(p sin<9, y = b r sin(p sin0, z = c r cos0,

w którym równanie elipsoidy

a

+

ma prostą postać

y^2	z^2 ,
p^+	“2 = ^1c
r^2 =	1.
wtedy	wartości

0

0

0

<P

2n,

a elementarna masa

dm = — dx dy dz = -—— abcr² sin(9 dr d0 dcp

V    4nabc

3 m 4k

r² sin® dr d0 d(p,

gdzie objętość elipsoidy obliczyliśmy ze wzoru:

1    * 2n

V

abcr² sin(9 dr d0 dcp =

0 0 0

^ TCflfec.

3

Zatem moment bezwładności względem osi x jest równy

h = p

(y² + z²) dx dy dz =

1 1C 2ic

3 m

47C

(ib²r² sin²</> sin²® +

ooo

m

+ c^zr² cos²<9) sin® r² dr d0 dcp = — (b² + c²).

5

Licząc analogicznie, otrzymujemy

e.

J, =

“ (a^2 + c^2),	h
h = Iz = h--	2 m
	^= T

m

= j (a² + fc²).

- i⁵