LABORATORIUM FIZYKI I |
Ćwiczenie nr 37 |
||
Wydział Mechatronika |
Grupa 21 |
Zespół 2 |
Data 27 - XI - 2003 |
Nazwisko i imię: Bartłomiej Korniluk
|
Przygotowanie |
||
Temat ćwiczenia: Falowe własności mikrocząsteczek sprawdzanie hipotezy de Broglie'a |
Zaliczenie |
||
Wstęp
Celem ćwiczenia było doświadczalne udowodnienie hipotezy de Broglie'a.
Hipoteza de Broglie'a: Każdej cząstce można przypisać falę o długości gdzie h - stała Plancka, a p - pęd cząstki.
W czasie ćwiczenia wykonywaliśmy podobne doświadczenie, jakie w 1927 roku przeprowadził G. P. Thomson, umieszczając w lampie oscyloskopowej, za układem anod ogniskujących, cienką złotą folię (folia o budowie polikrystalicznej).Elektrony padające na folię podlegały zjawisku interferencji dając na ekranie okręgi o różnych średnicach D. Zamiast folii złotej w doświadczeniu wykorzystaliśmy folie aluminiową i grafitową.
Schemat stanowiska pomiarowego
D1 D2
r
Stałe:
Plancka
masa elektronu
ładunek elektronu
Wyznaczam:
średnica okręgu interferencyjnego D [mm]
odległość folia ekran r [mm]
napięcie przyspieszające elektron U [kV]
odległość między płaszczyznami atomowymi d [m] przez pomiar średnicy wybranego rzędu pierścienia przy różnych napięciach przyspieszających
Folia grafitowa - sieć heksagonalna
odległość folia ekran: r = 127±1[mm]
błąd pomiaru ΔDi = 1 [mm]
niepewność napięcia
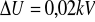
Wyniki dla wybranego prążka przy zmiennym napięciu przyspieszającym
Lp. |
x1 |
x2 |
Di = x2 - x1 |
Napięcie U [ kV ] |
|
1 |
30,5 |
47,5 |
17 |
9,04 |
0,010518 |
2 |
29,5 |
48,5 |
19 |
7,10 |
0,011868 |
3 |
29,5 |
49,5 |
20 |
6,28 |
0,012619 |
4 |
29 |
50 |
21 |
5,54 |
0,013435 |
5 |
28 |
51 |
23 |
4,42 |
0,015041 |
6 |
27 |
51,5 |
24,5 |
3,91 |
0,015992 |
Aby znaleźć odległość między płaszczyznami korzystamy z zależności ![]()
. Podstawiamy stałą ![]()
i zależność ![]()
aproksymujemy prostą.
Linear Regression for Data1_B:
Y = A + B * X
Parameter Value Error
------------------------------------------------------------
A 0,00301 3,47464E-4
B 2,33912 0,02598
------------------------------------------------------------
R SD N
------------------------------------------------------------
0,99925 1,17724E-4 6
------------------------------------------------------------
Otrzymujemy ![]()
.
Przekształcamy ![]()
Ostatecznie: 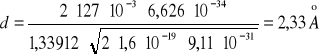
Błąd tej wartości obliczamy metodą różniczki zupełnej, przy założeniu że wartości h, m i e są wartościami wyznaczonymi bezbłędnie, tzn. błędy tych wartości w porównaniu z pozostałymi błędami są pomijalnie małe.
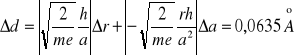
![]()
Wnioski
Wartość tablicowa odległości między płaszczyznami międzyatomowymi w folii grafitowej wynosi d = 1,42 ![]()
, a wliczona przez nas wartość jest nieco większa. Błąd pomiarów może wynikać głównie z niedokładności pomiaru średnicy okręgów oraz ich duża niepewność pomiarowa.
2. Folia aluminiowa - sieć kubiczna, powierzchnia centralna
Wyniki dla wybranego prążka przy zmiennym napięciu przyspieszającym
Lp. |
x1 |
x2 |
Di = x2 - x1 |
Napięcie U [kV] |
1/U |
1 |
18,6 |
21,4 |
2,8 |
12,31 |
0,009013 |
2 |
18,5 |
21,45 |
2,95 |
11,56 |
0,009301 |
3 |
18,35 |
21,45 |
3,1 |
10,98 |
0,009543 |
4 |
18,4 |
21,4 |
3 |
10,55 |
0,009736 |
|
18,3 |
21,45 |
3,15 |
10,13 |
0,009936 |
6 |
18,2 |
21,5 |
3,3 |
9,36 |
0,010336 |
Linear Regression for Data1_B:
Y = A + B * X
Parameter Value Error
------------------------------------------------------------
A -3,2641E-4 5,70216E-4
B 0,3501 0,05907
------------------------------------------------------------
R SD N
------------------------------------------------------------
0,94751 6,19138E-5 6
------------------------------------------------------------
Odległość miedzy płaszczyznami obliczamy analogicznie jak dla folii grafitowej.
Odległość folia - ekran wynosi: r = 300 [mm].
Otrzymujemy ![]()
.
Przekształcamy ![]()
Ostatecznie: 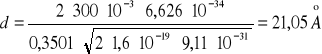
Błąd tej wartości obliczamy metodą różniczki zupełnej, przy założeniu że wartości h, m i e są wartościami wyznaczonymi bezbłędnie, tzn. błędy tych wartości w porównaniu z pozostałymi błędami są pomijalnie małe.
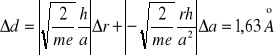
Musimy pomnożyć otrzymaną wartość przez 2 dla pierwszego okręgu ze względu na sieć kubiczną.
![]()
Wnioski
Wartość tablicowa odległości między płaszczyznami międzyatomowymi w folii grafitowej wynosi d = 4,04 ![]()
, a wliczona przez nas wartość różni się o jeden rząd wielkości. Błąd pomiarów może wynikać głównie z niedokładności pomiaru średnicy okręgów oraz ich duża niepewność pomiarowa.
Z uzyskanych wyników widać, siatka dyfrakcyjna potrzebna do zaobserwowania zjawiska interferencji cząstek takich jak elektrony musiała by mieć stałą (odległość między szczelinami ) rzędu nm. Wykonanie takiej siatki jest nie możliwe i dlatego najlepsze w tym przypadku są materiał będące w postaci krystalicznej. Zaobserwowane przez nas zjawisko jest podobne to tego, które uzyskał w 1927 roku G. P. Thomson.
Wyniki wskazują, że załamanie się elektronów odbywało na różnych płaszczyznach atomowych w krysztale. Widać to dla folii grafitowej, dla której zostały dokonane pomiary dwóch sąsiadujących pierścieni przy zmianie napięcia przyspieszającego. Z uzyskanych wyników widać, że odległości między płaszczyznami dla pierwszego pomiaru różnią się od odległości między płaszczyznami dla drugiego pomiaru. Do podobnego wniosku skłaniają wyniki pomiaru przeprowadzone dla kilku rzędów pierścieni przy stałym napięciu przyspieszającym. Wyniki obydwu pomiarów dla danego rodzaju folii oraz rzędu pierścieni są zgodne w granicach błędu.
1
4
Wyszukiwarka
Podobne podstrony:
C1, sprawozdanie c1, Laboratorium fizyki
sprawozdanie z laboratorium fizyki nr 37, Raport elegancki
Sprawozdanie z laboratorium z fizyki
PRAWO?RNULLIEGO Sprawozdanie z laboratorium z fizyki
sprawozdanie z laboratorium fizyki nr 28!, Raport elegancki
sprawozdania z fizyki, Sprawozdanie - Cwiczenie 2, Sprawozdanie z laboratorium z fizyki i biofizyki
Sprawozdanie z laboratorium z fizyki
bernuli-Notatek.pl, Sprawozdanie z laboratorium z fizyki
FIZYKA-sprawozdania, 22a, ĆWICZENIA LABORATORYJNE Z FIZYKI
3.1 b, Politechnika Lubelska, Studia, Studia, materiały na studia, Laboratorium fizyki, sprawozdani
Sprawozdanie 100a, Laboratorium Podstaw Fizyki
sprawozdanie z laboratorium fizyki nr 1, sprawka fizyka
EM 3.2, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, L
Sprawozdanie 64, Laboratorium Podstaw Fizyki
sprawozdania z fizyki, Sprawozdanie - Cwiczenie 9, Sprawozdanie z laboratorium z fizyki i biofizyki
W2 - SprawozdanieM, Laboratorium fizyki CMF PŁ
więcej podobnych podstron