OWAP
1.
Produkcja dwóch wyrobów [4]. Fabryka produkuje dwa wyroby A i B. Do produkcji tych wyrobów potrzebna jest praca maszyny M, surowiec S, oraz robocizna R. Fabryka dysponuje określonymi zdolnościami wytwórczymi podanymi w godzinach pracy maszyny, ograniczoną liczbą jednostek surowca oraz określoną liczbą roboczogodzin. W tablicy 1 podano ilości czasu pracy maszyny, ilości jednostek surowców oraz liczbę roboczogodzin potrzebnych do wytworzenia jednostki wyrobu.
Należy określić optymalny plan produkcji przyjmując jako kryterium maksymalny łączny zysk, mając podane zyski na jednostkę wyrobów: A i B odpowiednio 4 i 2 zł.
Tablica 1. Dane do przykładu 1
Środki |
Zużycie środków na jednostkę produkcji wyrobu |
Limity środków |
|
|
A |
B |
|
M |
2 |
2 |
2300 |
S |
14 |
4 |
10000 |
R |
3 |
2 |
4000 |
2.
BATONY [2]. Przedsiębiorstwo postanowiło uruchomić jednodniową produkcję próbną dwóch nowych batonów W1 i W2. Przedsiębiorstwo chce tak ustalić produkcję, aby z ich sprzedaży osiągnąć jak największy zysk. Na uruchomienie produkcji próbnej można przeznaczyć 6 godzin pracy urządzenia formującego batony oraz 240 kg masy bakaliowej, będącej jednym z podstawowych składników tych batonów. Postanowiono, że pracownicy oddelegowani do tej produkcji powinni zarobić, co najmniej 400 zł. W przedsiębiorstwie wielkość produkcji mierzy się masą produkcji, przyjmując 100 kg jako podstawową jednostkę pomiaru tej wielkości.
W tablicy podano jednostkowe nakłady czasu pracy urządzenia formującego batony, masy bakaliowej oraz robocizny, dotyczące produkcji obu rodzajów batonów. W ostatniej kolumnie podano wartości zysku, jaki zostanie osiągnięty ze sprzedaży 100 kg każdego rodzaju batonów przy aktualnych kosztach produkcji i zaplanowanych cenach zbytu.
Które wyroby i w jakich ilościach należy wyprodukować?
BATONY |
NAKŁADY JEDNOSTKOWE |
ZYSK, zł/j.pr. |
||
|
Pracy urządzeń, h/j.pr. |
Masy bakaliowej, kg/j.pr. |
Robocizny, zł/j.pr. |
|
W1 (Danek) |
2,0 |
40 |
100 |
480 |
W2 (Janek) |
1,2 |
60 |
200 |
210 |
Zasoby |
6 h |
240 kg |
400 zł |
|
3.
12 [1]. Przedsiębiorstwo może produkować cztery wyroby: A, B, C i D. Ograniczeniem w procesie produkcji są zasoby dwóch surowców: S1, S2. Niezbędne dane zawiera tablica.
Ceny wyrobów wynoszą odpowiednio: 10, 14, 8 i 11 zł. Ustalić wielkości produkcji tych wyrobów gwarantujące przy istniejących zasobach surowców maksymalny przychód z ich sprzedaży.
Surowce |
Zużycie surowca na jednostkę wyrobu, kg |
Zapas surowca, kg |
|||
|
A |
B |
C |
D |
|
S1 |
0,5 |
0,4 |
0,4 |
0,2 |
2 000 |
S2 |
0,4 |
0,2 |
0,0 |
0,5 |
2 800 |
4.
Zad.2 BM [3]. Fabryka produkuje cztery artykuły: A, B, C, D. Do produkcji tych artykułów potrzebna jest praca maszyn: M1, M2, M3, M4, surowce: P1, P2, P3 oraz robocizna, którą krótko oznaczymy przez R. Fabryka dysponuje określonymi zdolnościami wytwórczymi (podanymi w godzinach pracy maszyn w ciągu roku), określoną liczbą roboczo-godzin (również w ciągu roku) oraz ograniczoną liczbą surowców. W tablicy poniżej podano ilości czasu pracy maszyn, ilości surowców oraz liczbę roboczogodzin potrzebnych do wytworzenia jednostki produktu. Należy określić optymalny plan produkcji przyjmując jako kryterium sumaryczny zysk mając podane zyski na jednostkę produktów: A, B, C, D odpowiednio 2, 3, 6, 5 zł.
Środki |
Zużycie środków na jednostkę produkcji |
Limity środków |
|||
|
A |
B |
C |
D |
|
M1 |
2 |
5 |
0 |
0 |
3 000 |
M2 |
2 |
3 |
0 |
4 |
2 500 |
M3 |
0 |
6 |
7 |
3 |
3 200 |
M4 |
0 |
0 |
10 |
15 |
3 600 |
P1 |
10 |
15 |
23 |
16 |
25 000 |
P2 |
0 |
10 |
0 |
20 |
20 000 |
P3 |
30 |
0 |
20 |
5 |
30 000 |
R |
10 |
2 |
3 |
15 |
100 000 |
M
5.
Stop [8]. W fabryce należy wyprodukować stop o następujących własnościach:
Ciężar właściwy <= 1
Zawartość składnika s >= 10%
Temperatura topnienia >= 500 °C
Stop może być produkowany z surowców P1, P2, P3, których własności są podane w tablicy. Określić udział surowców P1, P2, P3 w mieszance, aby otrzymać stop o w/w właściwościach zakładając minimalny koszt produkcji.
Budując model matematyczny przyjąć upraszczające założenia o addytywności temperatury topnienia.
Własności |
P1 |
P2 |
P3 |
Ciężar właściwy |
0,9 |
0,95 |
1,02 |
Zaw. Składnika s, % |
8 |
12 |
15 |
Temp. Topnienia, °C |
550 |
500 |
490 |
Cena, zł/t |
100 |
300 |
50 |
6.
BMż4sur [3]. Do wytopu żeliwa używa się cztery gatunki surówek: S1, S2, S3, S4. Surówki te różnią się od siebie składem chemicznym i ceną zakupu, co przedstawia tablica.
Wiadomo, że do wytopu w żeliwiaku jeden nabój wsadu musi zawierać, co najmniej 10,2 kg Si, co najmniej 2,4 kg Mn oraz 2,7 - 4 kg P. Należy także uwzględnić, aby masowy udział siarki (S) w naboju wsadowym nie przekroczył 0,05%.
Określić optymalny skład naboju wsadowego mając na uwadze minimalny koszt wsadu.
Surówka |
Zawartości pierwiastków, % masowy |
Cena za 1 kg, zł/kg |
|||
|
Si |
Mn |
P |
S |
|
S1 |
2,6 |
0,4 |
0,6 |
0,04 |
5,0 |
S2 |
2,1 |
0,9 |
0,2 |
0,06 |
3,0 |
S3 |
2,1 |
0,6 |
0,6 |
0,05 |
4,0 |
S4 |
2,0 |
0,7 |
0,4 |
0,04 |
4,5 |
7.
3gat_w [3, 4]. Trzy gatunki węgla: A, B i C zawierają zanieczyszczenia fosforem i popiołem, W pewnym procesie przemysłowym potrzeba, co najmniej 100 T paliwa zawierającego nie więcej niż 0,03% fosforu i nie więcej niż 5% popiołu, Procent zanieczyszczeń i ceny zakupu poszczególnych gatunków węgla podano w tablicy.
Jak zmieszać wymienione gatunki węgla, aby uzyskać paliwo o możliwie najniższym koszcie, spełniające w/w wymagania?
Czy skład paliwa należy zmienić, jeżeli cena gatunku A wzrośnie o 15%?
Węgiel |
Zawartości zanieczyszczeń, % |
Cena zakupu 1T, zł |
|
|
Fosforu |
Popiołu |
|
A |
0,02 |
3 |
300 |
B |
0,05 |
5 |
280 |
C |
0,03 |
6 |
250 |
8.
(2.7.2. Namiarowanie wsadu [3, 4])
Do wytopu żeliwa o składzie chemicznym: Si - max 2,5%, Mn - max 0,65%, S - max 0,05%, Fe - reszta - używa się dwóch gatunków surówek: S1 i S2. Surówki te różnią się od siebie składem chemicznym i ceną zakupu. Ceny poszczególnych surówek oraz ich średni skład chemiczny zamieszczono w tablicy 7.
Należy określić optymalny skład mieszanki wsadowej do pieca indukcyjnego o pojemności 6 Mg, przy założeniu, że:
1) w procesie wytopu nie będzie strat,
2) w wyniku strat w procesie wytopu do stopu przechodzi 90% składników.
Tablica 7. Skład chemiczny i ceny surówek
|
%Si |
%Mn |
%S |
%Fe |
zł/kg |
S1 |
1,90 |
0,70 |
0,04 |
reszta |
5,8 |
S2 |
3,00 |
0,40 |
0,04 |
reszta |
4,3 |
R
9.
26 [1] Kłody o długości 5,6 m są cięte w tartaku na kawałki o długości: 1,2; 1,6; 1,9 m. Tartak ma wykonać dzienny plan produkcji, który zakłada oddanie, co najmniej 200 kłód o długości 1,2 m, 300 kłód o długości 1,6 m oraz 100 kłód o długości 1,9 m. W jaki sposób należy pociąć kłody, aby wykonać plan, a jednocześnie uzyskać jak najmniej odpadu. Za odpad przyjmuje się kawałki drewna krótsze niż 1,2 m. Zbudować i rozwiązać model matematyczny tego zagadnienia.
10.
2.8.1. Rozkrój kłód [4]. Tartak otrzymał zamówienie na dostarczenie 36 kompletów belek. Każdy komplet składa się z jednej belki długości 2,8 m, dwóch belek długości 2 m i czterech belek długości 1,6 m o tym samym przekroju. Tartak dysponuje kłodami o wymaganym przekroju i długości 6,5 m.
W jaki sposób pociąć kłody, aby wykonać zamówienie przy jak najmniejszym odpadzie? Ile kłód zostanie zużytych?
11.
28 [1] Zakład produkujący gwoździe otrzymuje drut o wymaganej grubości w 30 - centymetrowych kawałkach. Kawałki te cięte są na krótsze odpowiadające długością gwoździa, czyli 11, 8 i 5 cm. Należy tak pociąć otrzymane kawałki drutu, aby wyprodukować 12000 gwoździ o długości 11 cm, 24000 gwoździ o długości 8 cm i 27000 o długości 5 cm, minimalizując odpad.
12.
32 [1] Zakład produkujący puszki do konserw otrzymał surowiec w postaci dwóch rodzajów blachy: 21500 m blachy o szerokości 1,5 m i 14000 m blachy o szerokości 1,8 m. Z blachy wycinane są potrzebne elementy: denka i ściany boczne. Stosowane sposoby rozkroju 1 m blachy podano w tablicy. Zmaksymalizować liczbę otrzymanych puszek, pamiętając, że każda z nich ma dwa denka i jedną ścianę boczną. W jakim stopniu zostanie wykorzystana blacha obydwu rodzajów?
Elementy |
Sposoby rozkroju 1 m blachy |
|||||
|
o szerokości 1,5 m |
o szerokości 1,8 m |
||||
|
1 |
2 |
3 |
1 |
2 |
3 |
Denka |
70 |
15 |
10 |
30 |
20 |
- |
Ściany boczne |
- |
20 |
30 |
25 |
30 |
50 |
PI
13. [1]
14.
57 [1]. Kombinat metalurgiczny wytwarza na eksport dwa rodzaje stali: Z1 i Z2. Informacje decyzyjne pozwalające określić optimum asortymentowe produkcji na rok kalendarzowy zawarto w tablicy.
Wskazać taki asortymentowy plan produkcji stali Z1 i Z2, który przy możliwie najniższych kosztach własnych pozwoli uzyskać maksymalny wpływ dewizowy ze sprzedaży. Podać wysokość wpływu dewizowego przypadającego na 1 złotówkę kosztów własnych przy optymalnym rozwiązaniu.
Parametr |
Jednostka |
Stal |
Zasoby środków produkcji |
|
|
|
Z1 |
Z2 |
|
Zużycie surówki na 1 T stali |
T |
2,0 |
1,5 |
1 200000,0 |
Pracochłonność związana z produkcją 1 T stali |
h |
60,0 |
90,0 |
54000000,0 |
Zużycie innych surowców |
T |
0,3 |
0,3 |
270000,0 |
Koszt produkcji 1 T stali |
zł |
10000,0 |
15000,0 |
|
Cena eksportowa 1 T stali |
$ |
25000,0 |
50000,0 |
|
Minimalne zapotrzebowanie |
T |
150000,0 |
200000,0 |
|
Maksymalne zapotrzebowanie |
T |
700000,0 |
700000,0 |
|
ZZT
15.
67 [1]. Trzy składnice surowców wtórnych: I, II, III dostarczają te surowce do pięciu wykorzystujących je zakładów produkcyjnych. W składnicach znajduje się kolejno: 500, 700, 900 T surowca, a zdolności przerobowe zakładów produkcyjnych wynoszą: 400, 400, 700, 300, 300 T. W tablicy podano odległości pomiędzy składnicami a zakładami produkcyjnymi (w km).
Przy odległości do 200 km transport odbywa się samochodem (koszt 1 tonokilometra wynosi wówczas 8 zł). Jeżeli odległość jest większa niż 200 km korzysta się z transportu kolejowego, a koszt 1 tonokilometra wynosi wtedy 6 zł).
Opracować plan transportu surowców wtórnych ze składnic do zakładów przetwarzających surowce, tak, aby łączne koszty transportu były możliwie najniższe.
|
Zakłady produkcyjne |
||||
Składnice |
1 |
2 |
3 |
4 |
5 |
I |
130 |
250 |
330 |
170 |
400 |
II |
290 |
190 |
400 |
260 |
160 |
III |
150 |
350 |
240 |
190 |
210 |
16.
69 [1]. Trzech importerów hurtowników: H1, H2, H3 zaopatrują co 3 dni w banany cztery sklepy spożywcze: S1, S2, S3, S4. W czasie transportu część bananów ulega zepsuciu. Procentowy poziom ubytków bananów, zależny od czasu transportu, ofertę (podaż) dostawców (Ai) oraz zgłaszane zapotrzebowanie sklepów Bj (w kg) zawiera tablica. Zaplanuj taki sposób dostawy, który zapewni minimalizację zepsutych bananów.
|
O D B I O R C Y |
||||
DOSTAWCY |
S1 |
S2 |
S3 |
S4 |
Ai |
H1 |
2 |
3 |
4 |
1 |
2200 |
H2 |
5 |
7 |
3 |
2 |
2000 |
H3 |
1 |
4 |
8 |
3 |
2800 |
Bj |
1500 |
1400 |
2600 |
1500 |
|
17.
(3.1.1. Transport produktów [4])
Z dwóch magazynów M1 i M2 należy dostarczyć jednorodny produkt do pięciu sklepów: S1, S2, S3, S4 i S5. Znajdujący się w każdym magazynie zapas produktu ![]()
i zgłaszane zapotrzebowanie każdego sklepu ![]()
(w Mg) oraz jednostkowe koszty transportu z każdego magazynu do każdego sklepu ![]()
(w zł/Mg) są przedstawione w tablicy 13. Jak należy rozdzielić produkt, aby łączne koszty transportu były minimalne?
Tablica 13. Dane ZZT Transport produktów
Magazyny |
Sklepy |
|
||||
|
S1 |
S2 |
S3 |
S4 |
S5 |
|
M1 |
11 |
22 |
16 |
30 |
44 |
100 |
M2 |
20 |
35 |
18 |
36 |
54 |
130 |
|
55 |
40 |
65 |
50 |
20 |
|
OZT
18.
P16 [1]. Trzy magazyny: M, M2, M3 zaopatrują w mąkę cztery piekarnie P1, P2, P3 i P4. Jednostkowe koszty transportu (w zł za tonę), oferowane miesięcznie wielkości dostaw Ai (w tonach) oraz miesięczne zapotrzebowanie piekarni Bj (w tonach) podano w tablicy.
Podać plan przewozu i magazynowania nadwyżki mąki (ponad zapotrzebowanie piekarń) minimalizujący łączne koszty transportu i magazynowania. Jednostkowe koszty magazynowania wynoszą: w magazynie M1 - 5 zł (c15=5), w magazynie
M2 - 5 zł (c25=5) i w magazynie M3 - 6 zł (c35=6) za tonę.
Magazyny |
Piekarnie |
Ai, T |
|||
|
P1 |
P2 |
P3 |
P4 |
|
M1 |
50 |
40 |
50 |
20 |
100 |
M2 |
40 |
80 |
70 |
30 |
50 |
M3 |
60 |
40 |
70 |
80 |
80 |
Bj, T |
40 |
60 |
50 |
50 |
|
19.
70 [1]. Cztery zakłady dziewiarskie: Z1, Z2, Z3 i Z4 zaopatrują się we włóczkę w trzech hurtowniach:H1, H2 i H3. Zapotrzebowanie zakładów wynosi kolejno: 600, 500, 400 i 700 kg włóczki miesięcznie, natomiast poszczególne hurtownie maja na składzie 1200, 800 i 1000 kg włóczki. Jednostkowe koszty transportu pomiędzy hurtowniami a zakładami zestawiono w tabl. 93. Włóczka, która nie została sprzedana w miesiącu, będzie magazynowana w hurtowniach, przy czym jednostkowe koszty magazynowania wynoszą odpowiednio 2, 1 i 2 zł miesięcznie.
Podać optymalny plan transportu i magazynowania włóczki, minimalizujący łączne koszty transportu i magazynowania.
Podać łączną wysokość kosztów oraz dokonać ich rozliczenia na transport i magazynowanie.
Hurtownie |
Zakłady |
|||
|
Z1 |
Z2 |
Z3 |
Z4 |
H1 |
6 |
4 |
3,5 |
5 |
H2 |
5,5 |
4,5 |
4,5 |
4 |
H3 |
6 |
8,5 |
2,5 |
8 |
20.
(3.2.1. Transport cegieł[4])
Przedsiębiorstwo posiadające trzy cegielnie w miejscowościach: C1, C2 i C3 dostarcza cegłę do czterech hurtowni materiałów budowlanych: H1, H2, H3 i H4. Okresową ilość oferowanych cegieł ![]()
, zgłaszane zapotrzebowanie hurtowni ![]()
(w Mg) i jednostkowe koszty transportu z każdej cegielni do każdego magazynu hurtowego ![]()
(w zł/Mg) przedstawiono w tablicy 15. Jaki powinien być plan przewozów, aby zminimalizować łączne koszty transportu?
Tablica 15. Dane OZT Transport cegieł
Cegielnie |
Hurtownie |
|
|||
|
H1 |
H2 |
H3 |
H4 |
|
C1 |
24 |
36 |
57 |
87 |
14 |
C2 |
18 |
33 |
45 |
66 |
16 |
C3 |
30 |
69 |
63 |
42 |
22 |
|
12 |
8 |
14 |
10 |
|
ZT-P
21.
?? [1]. Trzy zakłady produkcyjne Z1, Z2 i Z3 zaopatrują w produkt pięciu odbiorców: O1, O2, O3, O4 i O5. Zdolności produkcyjne zakładów wynoszą odpowiednio: 5000, 6000 i 4000 jedn., a zapotrzebowanie odbiorców jest następujące: 4000, 3000, 2000, 1000 i 3000 jedn. Jednostkowe koszty produkcji w poszczególnych zakładach kształtują się na poziomie 220, 200 i 210 zł, a jednostkowe koszty transportu (w zł) podano w tablicy ZT1.
Tablica ZT1. Jednostkowe koszty transportu (w zł)
|
Odbiorcy |
||||
Zakłady |
O1 |
O2 |
O3 |
O4 |
O5 |
Z1 |
5 |
12 |
10 |
8 |
10 |
Z2 |
5 |
7 |
15 |
10 |
14 |
Z3 |
8 |
13 |
7 |
16 |
9 |
Opracować optymalny plan produkcji i przewozu produktu między dostawcami i odbiorcami, zakładając:
a) możliwość nieograniczonego zbytu towaru, w związku z czym zdolności produkcyjne zakładów będą wykorzystane, a nadwyżka towaru ponad zapotrzebowanie odbiorców będzie magazynowana (jednostkowe koszty magazynowania w poszczególnych zakładach wynoszą odpowiednio: 2, 3 i 3);
b) wykorzystanie zdolności zakładów tylko w takim zakresie, w jakim tego wymaga zapotrzebowanie odbiorców.
22.
P17 [1]. Dostawcami mąki do piekarń (P1, P2, P3 i P4) są jej bezpośredni producenci - młyny (M1, M2, M3), a parametry Ai są potencjalnymi zdolnościami produkcyjnymi młynów. Obok jednostkowych kosztów transportu (w zł za tonę), podane są koszty produkcji mąki (hi w zł/T) w poszczególnych młynach.
Podać optymalny plan produkcji i transportu mąki z młynów do piekarń, tak, aby zminimalizować łączne koszty produkcji, transportu i magazynowania mąki.
(Jednostkowe koszty magazynowania wynoszą: w magazynie M1 - 5 zł (c15=5), w magazynie M2 - 5 zł (c25=5) i w magazynie M3 - 6 zł (c35=6) za tonę).
Młyny |
Piekarnie |
Ai |
hi |
|||
|
P1 |
P2 |
P3 |
P4 |
|
|
M1 |
50 |
40 |
50 |
20 |
100 |
1080 |
M2 |
40 |
80 |
70 |
30 |
50 |
1060 |
M3 |
60 |
40 |
70 |
80 |
80 |
1100 |
Bj |
40 |
60 |
50 |
50 |
|
|
23.
73 [1]. Trzy kopalnie K1, K2 i K3 dostarczają węgiel do pięciu składów opału: S1, S2, S3, S4 i S5 położonych w różnych miejscowościach. Każdy ze składów może przyjąć 400 T węgla miesięcznie, natomiast możliwości wydobywcze kopalń wynoszą:
K1 - 600T, K2 iK3 - po 700T miesięcznie. Koszty wydobycia 1T węgla w kopalniach wynoszą odpowiednio 108, 96 i 102 zł miesięcznie, natomiast jednostkowe koszty transportu w zł za tonę (zależnie od odległości) podano w tablicy.
Ustalić plan przewozu węgla, mający na celu minimalizację łącznych kosztów wydobycia i transportu węgla.
|
Składy opału |
|
|
|
|
Kopalnie |
S1 |
S2 |
S3 |
S4 |
S5 |
K1 |
14 |
5 |
9 |
24 |
15 |
K2 |
30 |
24 |
11 |
8 |
19 |
K3 |
9 |
22 |
15 |
7 |
18 |
ZLP
24.
78 [1]. Zaproponować lokalizację 4-ch punktów skupu zboża, które dostarczyłyby skupione zboże do trzech młynów: M1, M2, M3.
Ustalono, że punkty skupu można zlokalizować w gminach: G1, G2, G3 i G4, przy czym każdy z nich może skupić 40 t zboża. Natomiast zapotrzebowanie młynów wynosi: 35, 35 i 50 t. Jako kryterium optymalizacji należy przyjąć minimalizację odległości, przy czym odległości pomiędzy punktami skupu a młynami (w km) podano w tablicy.
PUNKTY skupu |
MŁYNY |
||
|
M1 |
M2 |
M3 |
G1 |
25 |
38 |
43 |
G2 |
29 |
16 |
51 |
G3 |
60 |
42 |
13 |
G4 |
44 |
33 |
22 |
MPP
25.
P19 [1]. Zminimalizować puste przebiegi samochodów o ładowności 50t, przewożących drobnicę pomiędzy siedmioma miastami stanowiącymi układ zamknięty. Dzienne przywozy pi i wywozy wi drobnicy do i z poszczególnych miast w tonach oraz odległości pomiędzy tymi miastami podano w tablicy.
Dij |
L |
M |
N |
O |
P |
R |
S |
wi' |
L |
0 |
20 |
50 |
100 |
150 |
200 |
100 |
1000 |
M |
|
0 |
40 |
20 |
30 |
50 |
20 |
2000 |
N |
|
|
0 |
100 |
150 |
200 |
100 |
1000 |
O |
|
|
|
0 |
40 |
30 |
150 |
100 |
P |
|
|
|
|
0 |
80 |
70 |
200 |
R |
|
|
|
|
|
0 |
60 |
1000 |
S |
|
|
|
|
|
|
0 |
500 |
pi' |
500 |
1000 |
2000 |
1000 |
1000 |
300 |
0 |
5800 |
26.
83 [1]. Przedsiębiorstwo transportowe odnajmuje ciężarówki o jednakowej ładowności, które przewożą towary pomiędzy siedmioma miastami. Przewidywany przewóz masy towarowej pomiędzy tymi miastami (wyrażony liczbą pełnych ciężarówek) podaje tablica 105, a odległości między miastami (w km) zestawiono w tablicy 106.
Znaleźć taki plan przewozu pustych ciężarówek, przy którym samochodokilometraż pustych przebiegów będzie minimalny.
Tablica 105. Przewóz z miasta i do miasta j (liczba ciężarówek)
i j |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
0 |
5 |
8 |
11 |
4 |
6 |
16 |
2 |
10 |
0 |
8 |
7 |
6 |
5 |
12 |
3 |
9 |
4 |
0 |
5 |
5 |
10 |
7 |
4 |
4 |
3 |
3 |
0 |
6 |
9 |
17 |
5 |
20 |
15 |
4 |
9 |
0 |
8 |
6 |
6 |
10 |
9 |
7 |
8 |
11 |
0 |
11 |
7 |
8 |
7 |
6 |
5 |
7 |
9 |
0 |
Tablica 106. dij - odległości między miastami, km
Dij |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
0 |
18 |
34 |
55 |
10 |
21 |
50 |
2 |
|
0 |
53 |
29 |
64 |
19 |
10 |
3 |
|
|
0 |
18 |
33 |
22 |
14 |
4 |
|
|
|
0 |
54 |
9 |
36 |
5 |
|
|
|
|
0 |
13 |
15 |
6 |
|
|
|
|
|
0 |
19 |
7 |
|
|
|
|
|
|
0 |
Problemy przydziału
27.
P 22 [1]. W dużym przedsiębiorstwie cztery sekretarki należy przydzielić do prowadzenia czterech różnych prac biurowych. Z ostatnich zapisów znany jest czas (w min), jaki zajmuje tym sekretarkom wykonywanie poszczególnych prac, który podano w tablicy.
Zakładając specjalizację sekretarek, tzn., że każda z nich będzie wykonywać tylko jedną pracę, określić optymalny przydział z punktu widzenia minimalizacji łącznego czasu wykonywania prac.
|
Czas niezbędny przy wykonywaniu pracy, min |
|||
Sekretarka |
1 |
2 |
3 |
4 |
1 |
420 |
480 |
240 |
360 |
2 |
480 |
420 |
300 |
360 |
3 |
420 |
540 |
300 |
420 |
4 |
360 |
480 |
360 |
480 |
28.
89w5 [1]. W elektrociepłowni pracują trzy agregaty: A1, A2 i A3, które wykorzystują dwa rodzaje paliwa, W tablicy podano uzysk energii cieplnej z 1 t paliwa.
|
Uzysk energii (w Gcal) |
|
Agregaty |
p1 |
p2 |
A1 |
5 |
7 |
A2 |
6 |
4 |
A3 |
3 |
5 |
Plan produkcyjny zakłada wytworzenie, co najmniej 4200 Gcal, przy czym ze względów technicznych dokładnie połowa wytworzonej ilości energii powinna pochodzić z agregatu pierwszego. Ponadto wiadomo, że każdego rodzaju paliwa nie będzie można nabyć więcej niż 330 t, a ceny nabycia 1 t paliwa wynoszą odpowiednio 440 i 650 zł.
Opracować optymalny plan zakupu Paliwa oraz przydziału do poszczególnych agregatów, minimalizujący koszty zakupu paliwa.
29.
92w5 [1]. Pewna firma dysponuje m/in. trzema samochodami. Postanowiono wymienić je na nowe. Zdecydowano, że stare zostaną zaproponowane pracownikom firmy. Ogłoszono przetarg, w którym oferty z propozycją ceny, jaką są gotowi zapłacić (tys. zł), złożyło czterech pracowników.
Znaleźć optymalny przydział samochodów poszczególnym pracownikom tak, aby zmaksymalizować dla firmy przychód ze sprzedaży samochodów. Podać wysokość tego przychodu.
Oferta pracownika |
Samochody |
||
|
Ford |
Mercedes |
Polonez |
A |
19 |
35 |
15 |
B |
21 |
39 |
12 |
C |
18 |
40 |
14 |
D |
20 |
26 |
16 |
30.
PES [5]. Urząd pocztowy ma zapotrzebowanie na różną liczbę pracowników pełnoetatowych w różnych dniach tygodnia.
Liczba pełnoetatowych pracowników wymaganych każdego dnia jest przedstawiona w tablicy. Uregulowania związków zawodowych stanowią, że każdy pełnoetatowy pracownik musi pracować 5 kolejnych dni i wtedy otrzymuje 2 dni wolnego, np. pracownik, który pracuje od poniedziałku do piątku musi otrzymać wolne w sobotę i w niedzielę. Urząd pocztowy chce osiągnąć swoje dzienne zapotrzebowanie korzystając tylko z pełnoetatowych pracowników. Jego celem jest zminimalizowanie liczby pełnoetatowych pracowników, która musi być zatrudniona.
Tablica. Zapotrzebowanie pracowników w Urzędzie Pocztowym
|
minimum wymaganych pracowników |
Poniedziałek |
17 |
Wtorek |
13 |
Środa |
15 |
Czwartek |
19 |
Piątek |
14 |
Sobota |
16 |
Niedziela |
11 |
G
Gry dwuosobowe o sumie zero
31.
P 25 [1]. Przedsiębiorstwo produkcyjne A może uruchomić produkcję produktu w wysokości 100, 200, 300 tys. szt. Konkurencyjne przedsiębiorstwo B może postąpić w ten sam sposób. W tablicy podano zyski (w tys. zł) przedsiębiorstwa A (straty przedsiębiorstwa B) przy produkcji wyrobu w zależności od decyzji podjętych przez przedsiębiorstwa.
Podjąć decyzję o wielkości produkcji, będąc menadżerem przedsiębiorstwa A.
|
B1 |
B2 |
B3 |
A1 |
10 |
230 |
50 |
A2 |
150 |
250 |
140 |
A3 |
80 |
200 |
220 |
32.
P 26 [1]. Rozwiązać grę dwuosobową o sumie zero, której macierz wypłat dana jest w tablicy. Podać optymalną strategię dla gracza A oraz wartość gry.
|
B1 |
B2 |
B3 |
A1 |
-2 |
8 |
2 |
A2 |
3 |
-1 |
0 |
33.
P 25w5 [1]. Dwaj producenci pewnego wyrobu sprzedają swe wyroby na rynku, którego wielkość jest stała. Aby zwiększyć swój udział w rynku (przejąć część klientów konkurencyjnego przedsiębiorstwa), każde z nich może zastosować jedną z trzech strategii marketingowych. Strategie przedsiębiorstwa A to A1, A2 i A3, a strategie przedsiębiorstwa B to B1, B2 i B3. W tablicy podano wzrost udziału w rynku (w %) przedsiębiorstwa A (spadek udziału przedsiębiorstwa B) w zależności od decyzji podjętych przez przedsiębiorstwa. Znaleźć optymalne strategie dla obu przedsiębiorstw.
|
B1 |
B2 |
B3 |
A1 |
3 |
-3 |
7 |
A2 |
-1 |
5 |
2 |
A3 |
0 |
-4 |
4 |
Gry z naturą
34.
P27 [1]. Rolnik posiadający glebę klasy III ma wybrać pod uprawę jeden z trzech rodzajów zboża. Plony tych zbóż z 1 ha w kwintalach, w zależności od warunków klimatycznych w przyszłym roku, zawiera tablica. Który z rodzajów zbóż rolnik powinien wybrać pod uprawę?
Stany natury |
B1 |
B2 |
B3 |
B4 |
Zboże |
|
|
|
|
Żyto |
24,5 |
18,0 |
18,0 |
16,0 |
Pszenica |
18,0 |
32,0 |
24,0 |
21,0 |
Jęczmień |
15,0 |
19,0 |
26,0 |
19,0 |
PN
35.
Przykład zad5 [3, 4].
Dla dwóch funkcji:
![]()
i ![]()
1. Rozwiązać zagadnienia optymalizacji:
1.1) ![]()
1.2) ![]()
z warunkiem ograniczającym:
![]()
przyjmując kolejno następujące punkty startowe: ![]()
; ![]()
; ![]()
; ![]()
.
2. Wygenerować w arkuszu kalkulacyjnym punkty dla obu funkcji oraz sporządzić ich wykresy. Generując punkty należy przyjąć krok ![]()
oraz założyć, że ![]()
.
3. Porównać uzyskane wyniki optymalizacji z wykresami funkcji.
Wskazać ekstrema lokalne i ekstrema globalne.
36.
Zad. 1 [6].
Zagadnienie optymalizacji nieliniowej z ograniczeniami równościowymi
i nierównościowymi [6]:
Liczba zmiennych: 3
Ograniczenia: 1 ograniczenie równościowe, nieliniowe
1 ograniczenie równościowe, liniowe
3 graniczenia dla zmiennych niezależnych
Min ![]()
z ograniczeniami:
![]()
![]()
![]()
![]()
Punkt startowy niebędący rozwiązaniem dopuszczalnym:
![]()
![]()
![]()
Rozwiązanie:
![]()
![]()
37.
Zad. 2 [6]
Zagadnienie optymalizacji nieliniowej z ograniczeniami [6]:
Liczba zmiennych: 5
Liczba ograniczeń: 6 ograniczeń nieliniowych, nierównościowych
10 ograniczeń dla zmiennych niezależnych
Uwaga: zmienne ![]()
nie występują w definicji funkcji celu ![]()
Funkcja celu:
Min: ![]()
= ![]()
Ograniczenia:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Punkt startowy będący rozwiązaniem dopuszczalnym:
![]()
![]()
Rozwiązanie:
![]()
![]()
Punkt startowy niebędący rozwiązaniem dopuszczalnym:
![]()
![]()
Rozwiązanie:
![]()
dla ![]()
jak wyżej
38.
Zad. 3 [6].
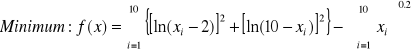
Ograniczenia:
![]()
, ![]()
Punkt początkowy:
![]()
, ![]()
39.
Zad. 4 [6]
Minimum: ![]()
Ograniczenia:
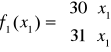
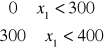
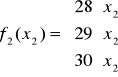
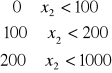
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Punkt początkowy:
![]()
![]()
Rozwiązanie:
![]()
![]()
40.
P 36 [1]. Z elektrowni energia przesyłana jest do dwóch zużywających ją zakładów produkcyjnych. Funkcja kosztów przesyłania energii do tych zakładów w zależności od wielkości przesyłu (odpowiednio, do zakładu I - x1 i do zakładu II - x2) dana jest wzorem:
![]()
Rozdzielić dzienną produkcję energii wynoszącą 16 MWh pomiędzy te dwa zakłady tak, aby zminimalizować koszty przesyłu energii. Podać wysokość tych kosztów.
41.
P 37 [1]. Rozwiązać następujące zadanie:
![]()
przy warunkach:
![]()
,
![]()
.
42.
150 [1]. Przedsiębiorstwo przemysłowe korzysta z dwóch bocznic: własnej i PKP. Koszty (w tys. zł) związane z postojem wagonów wyraża następująca funkcja:
![]()
,
gdzie ![]()
oznacza czas trwania wyładunku na bocznicy własnej, ![]()
- czas trwania wyładunku na bocznicy PKP.
Pociągi towarowe wożące surowce do przedsiębiorstwa mają w swym składzie 100 wagonów. Dzienna zdolność przeładunkowa bocznicy własnej wynosi 10 wagonów, a bocznicy PKP - 20 wagonów.
1. Jak należy rozdzielić wagony między obie bocznice, aby koszt związany z postojowym był możliwie najniższy?
2. Ile dni wobec tego będzie trwał wyładunek na bocznicy własnej, a ile na bocznicy PKP?
3. Podać koszt postojowego przy optymalnym rozłożeniu wagonów między obie bocznice,
Zakładamy, że z wyładowanych wagonów formuje się skład pociągu, który może odejść dopiero wtedy, gdy wszystkie wagony są opróżnione, Tym samym postojowe liczy się do momentu wyładunku ostatniego z wagonów na każdej z bocznic.
43.
163 [1]. Planowane są prace modernizacyjne w trzech kopalniach. Rezultatem tych prac ma być łącznie 15 tys. ton przyrostu dziennego wydobycia. Koszty prac modernizacyjnych w zależności od planowanego przyrostu wydobycia w poszczególnych kopalniach (odpowiednio x1, x2, x3) wyraża funkcja:
![]()
.
Zaplanować wielkości przyrostu wydobycia dla poszczególnych kopalń tak, aby koszty prac modernizacyjnych były możliwie najniższe. Podać wysokość tych kosztów.
44.
3.4. [7]. Dane są 3 bloki energetyczne, dla których krzywe kosztów (tj. ilość gramów paliwa umownego przypadające na 1 kWh wyprodukowanej energii w funkcji mocy oddanej z tego bloku P w MW) zdjęte doświadczalnie podane są na wykresie.
Przyjąć, że w przybliżeniu krzywe wykreślone aproksymowane są przez:
![]()
![]()
![]()
A) Określić optymalny rozkład obciążeń na poszczególne bloki przy założeniu, że sumaryczna moc zespołu wynosi 300 MW.
B) Rozwiązać powyższy problem przy dodatkowym założeniu, że maksymalna wydajność poszczególnych bloków energetycznych wynosi 110 MW.
Literatura
1. Jędrzejczyk Z., Skrzypek J., Kukuła K., Walkosz A.: Badania operacyjne w przykładach i zadaniach; pod red. K. Kukuły, wyd. piąte, PWN, Warszawa 2004.
2. Szapiro T., Kuszewski T., Nykowski I., Dubnicki W., Gąsiorowski P., Ożdżeński W.: Decyzje menedżerskie z Excelem; praca zbiorowa pod red. T. Szapiro, PWE Warszawa 2000.
3. Machulec B.; praca niepublikowana.
4. Węgrzyn J.: Elementy badań operacyjnych w arkuszu kalkulacyjnym, Wydawnictwo Politechniki Śląskiej, Gliwice 2010.
5. Winston W. L., Albright S. C.: Practical Management Science, 2nd edition, Duxbury an imprint of Brooks/Cole Thompson Learning, USA 2003.
6. Himmelblau D. M.: Applied Nonlinear Programming, McGraw-Hill Book Company, 1972.
7. Zbiór zadań z teorii systemów i teorii sterowania, praca zbiorowa pod red. J. Klamki, Wyd. Pol. Śl., Gliwice 1979.
8. ? źródło nie ustalonne
1: 2,
2: 1,
3: 27, (OWAP 1, M 0, R 3, PI 2, ZZT 2, OZT 2, ZT-P 3, ZLP 1, MPP 2, PP 3, G 4, PN 4)
4: 4,
5: 4,
6: 1,
7: 1.
8: 1.
UWAGA
Addytywność. Matematyczna własność wielkości polegająca na tym, że jej wartość odpowiadająca całemu obiektowi równa jest sumie wartości tej wielkości odpowiadających częściom obiektu przy dowolnym podziale jego na części.
W przypadku zagadnienia optymalnego wyboru asortymentu produkcji w odniesieniu do funkcji celu założenie addytywności pozwala przedstawić łączny zysk jako sumę zysków otrzymanych z wytworzenia pojedynczych wyrobów. Z kolei łączne zużycie każdego środka produkcji wyrażane przez dany warunek ograniczający jest sumą zużycia tego środka na produkcję różnych wyrobów, do produkcji których środek ten się zużywa.
Wg http://pl.wikipedia.org/wiki/Funkcja_addytywna#Definicje
Zakładając, że
![]()
,
gdzie: ![]()
temperatura składnika i,
![]()
udział masowy i-tego składnika w mieszaninie do sporządzenia stopu,
to ![]()
,
a suma wszystkich udziałów składników ![]()
,
to ![]()
, czyli ![]()
23
15
zad3 A_M_R_PI_ZT_G_PN_BM.doc
Wyszukiwarka
Podobne podstrony:
Ćwiczenie 3 - kompozyty, Studia, SEMESTR 7, PI, materiały
2011 KK3 PI ćwiczenia 2 akcje 1
Ćwiczenie BM
cwiczenia 3, wzor zad3, Dyplom
ćwiczenie 01 pn
cwiczenie 1 PN
cwiczenia 3, 2BGG4 Krutys Kufrasa zad3, Dyplom
Zad3, ►► UMK TORUŃ - wydziały w Toruniu, ►► Socjologia, Praca socjalna, Polityka społeczna, ćwiczeni
3 ćwiczenia BADANIE asfaltów
Ćwiczenie7
Cwiczenia 2
Ćwiczenia V
metody redukcji odpadów miejskich ćwiczenia
Ćwiczenia1 Elektroforeza
więcej podobnych podstron