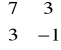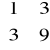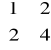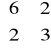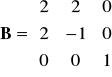Zadania z matematyki dla studentów I - go roku studiów stacjonarnych
Zestaw 10
Diagonalna postać macierzy przekształcenia liniowego
1. |
Wykaż, że każda macierz skośno-symetryczna stopnia trzeciego ma tylko jedną wartość własną. |
2. |
Znajdź wielomiany charakterystyczne macierzy:
A = |
3. |
Znajdź wartości własne macierzy A,
A = |
4. |
Wykaż, że jeżeli |
5. |
Znajdź wartości własne i wektory własne macierzy przekształceń liniowych:
A = Zapisz macierze przekształceń w postaci diagonalnej. |
6. |
Znajdź bazę, w której macierz przekształcenia liniowego A przyjmie postać diagonalną
A = |
7. |
Wykaż, że wartość wyznacznika macierzy przekształcenia liniowego nie zależy od wy- boru bazy, w której zapisano to przekształcenie. |
8. |
Macierz A =
detA = |
Wyszukiwarka
Podobne podstrony:
matma zad, Z3, Zadania z matematyki dla studentów I-go roku studiów stacjonarnych
matma zad, Z11, Zadania z matematyki dla studentów I - go roku studiów stacjonarnych
matma zad, Z4, Zadania z matematyki dla studentów 1-go roku studiów stacjonarnych
matma zad, Z17, Zadania z matematyki dla studentów 1 - go roku
matma zad, Z12, Zadania z matematyki dla studentów 1 - go roku
matma zad, Z7(2), Zadania z matematyki dla studentów 1- go roku
matma zad, Z5, Zadania dla studentów 1-go roku
matma zad, Z7J, ZADANIA Z MATEMATYKI
matma zad, Z7J, ZADANIA Z MATEMATYKI
Zad MECH-IZR ESO II, Przykładowe zadania przygotowawcze dla studentów Wydziału Mechanicznego
Zadania i odpowiedzi, Zad.MST-09, Matematyka dla MSB
Zadania i odpowiedzi, Zad.MST-05, Zadania z MATEMATYKI dla pierwszego roku
Zadania z matematyki dla 3 roku dziennych, Uczelnia
Zadanie-podatki-dla studentów 2010, Ogrodnictwo, Semestr V, Ekonomika, Ekonomika z chomika ;)
jajo matematyczne, karty pracy dla klas I-III, zadania matematyczne dla kl.1
więcej podobnych podstron