Zestaw VII

Różniczka i badanie funkcji

1. Wyznacz różniczki funkcji:
,
.

2. Wykorzystując pojęcie różniczki funkcji oblicz przybliżoną wartość
,
,
.

3. Rozwiń w szereg Maclaurina funkcje:
i

4. Korzystając z rozwinięcia Maclaurina wyznaczyć liczbę e z dokładnością do 0,0001 oraz
z dokładnością do 0,001.

5. Wyznaczyć różniczkę zupełną funkcji
w punkcie
.

6. Wyznacz różniczkę drugiego rzędu dla funkcji:

;
.

7. Wykorzystując pojęcie różniczki oblicz:

a) przybliżoną wartość funkcji w punkcie (1,01; 2,03); b) przybliżoną wartość wyrażenia
.

c) przybliżoną wartość przyrostu funkcji
jeżeli x zmienia się od 2 do 2,1, a y od 3 do 2,5.

8. Funkcja produkcji fikcyjnego przedsiębiorstwa ma postać
, gdzie - wartość produkcji, x - zatrudnienie mierzone funduszem płac, y - wartość środków trwałych. Jak zmieni się wartość produkcji, jeżeli zatrudnienie zwiększy się o 3% (przy założeniu, że wartość środków produkcji nie ulegnie zmianie)?

9. Wyznacz elastyczność funkcji:
,
.

10. Dla podanych funkcji wskazać punkty, w których mogą one mieć ekstrema lokalne:
;
,
.

11. Wyznaczyć przedziały monotoniczności i ekstrema funkcji:
;
;
;
;
.

12. Wyznaczyć największą i najmniejszą wartość funkcji a)
w przedziale
;

b)
w przedziale
; c)
dla
.

13. Wyznaczyć przedziały wklęsłości i wypukłości oraz punkty przegięcia funkcji:
;
;
;
;
.

14. Naszkicuj wykresy funkcji: a)
. b)
. c)
.

15. Zbadaj przebieg zmienności funkcji:
;
;
;

16. Funkcja kosztów całkowitych fikcyjnego przedsiębiorstwa określona jest wzorem
gdzie x oznacza wielkość produkcji. Zakład sprzedaje towar po cenie p zależnej od wielkości produkcji według wzoru
.

a) przy jakiej wielkości produkcji zysk przedsiębiorstwa będzie największy?

b) wyznaczyć funkcję kosztów przeciętnych i krańcowych,

c) przy jakiej wielkości produkcji koszty przeciętne są równe kosztom krańcowym.

17. Okno o obwodzie l ma kształt prostokąta zakończonego półkolem. Jakie powinny być wymiary okna, aby ilość światła przenikającego przez nie była największa?

18. Z prostokątnego kawałka blachy o szerokości s należy wygiąć rynnę o przekroju prostokątnym w taki sposób, aby mogło nią spływać możliwie najwięcej wody. Znaleźć wymiary przekroju tej rynny.

19. Wyznaczyć ekstrema lokalne funkcji:

a)
b)

c)
d)

20. Dany jest trójkąt o wierzchołkach (-1; 2), (0; 4), (2; 3). Wyznaczyć taki punkt S, dla którego suma kwadratów odległości od wierzchołków trójkąta jest najmniejsza.

21. Wyznaczyć ekstrema globalne funkcji
jeżeli: a)
; b)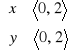

22. Wyznaczyć ekstremum funkcji
dla punktów leżących na prostej
.

23. Znaleźć ekstrema lokalne funkcji
na brzegu obszaru
.

2