Zadania z matematyki dla Towaroznawstwa
Zestaw IX
1. Zakładamy, że gospodarka składa się z dwóch gałęzi i macierz współczynników nakładów (kosztów) ma postać ![]()
. Natomiast popyt zewnętrzny na poszczególne produkty wynosi odpowiednio 11 i 5 (w mld zł). Wyznaczyć potrzebną wielkość produkcji poszczególnych gałęzi.
2. Zakładamy, że gospodarka składa się z trzech gałęzi i macierz współczynników nakładów (kosztów) ma postać 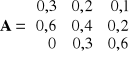
. Natomiast popyt zewnętrzny na poszczególne produkty wynosi odpowiednio 10, 4 i 5 (w mld zł). Wyznaczyć potrzebną wielkość produkcji poszczególnych gałęzi.
3. Sporządzić tablicę przepływów międzygałęziowych, jeśli podana jest macierz współczynników kosztów 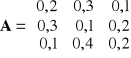
. Wiemy ponadto, że wektor produkcji globalnych jest równy 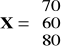
. Jak zmienią się wartości produktów końcowych, jeśli wartość produkcji globalnej drugiej gałęzi wzrośnie o 20 j.p.?
4. Dana jest tablica przepływów międzygałęziowych:
|
1 |
2 |
3 |
|
|
i |
|
|
|
|
|
1 |
10 |
20 |
30 |
40 |
100 |
2 |
20 |
40 |
60 |
80 |
200 |
3 |
20 |
50 |
90 |
140 |
300 |
obliczyć, o ile wzrosną produkty końcowe w każdej gałęzi, jeżeli produkcje globalne wzrosną o
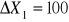
,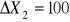
,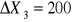
j.p.o ile powinny wzrosnąć produkcje globalne każdej gałęzi, jeśli popyt zewnętrzny na poszczególne produkty zmieni się odpowiednio o
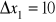
,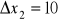
,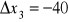
j.p.?
5. Dla dwudziałowej gospodarki wiadomo, że: dział I do wyprodukowania dobra A o wartości 1 zł zużywa swój produkt o wartości 10 gr i dobro B o wartości 60 gr; dział II do wytworzenia dobra B o wartości 1 zł nie zużywa własnego produktu, tylko dobro A o wartości 50 gr; popyt na dobro A wynosi 1000 mln zł, a na dobro B - 2000 mln zł. Wyznaczyć poziom produkcji globalnej obu działów, zaspokajający popyt.
Wyszukiwarka
Podobne podstrony:
Zadania i odpowiedzi, Zad.MST-05, Zadania z MATEMATYKI dla pierwszego roku
Zadania i odpowiedzi Zad.MST-07
Zadania i odpowiedzi, Zad.MST-06, 2010/2011
Zadania i odpowiedzi, Zad.MST-08
Zadania i odpowiedzi, Zad.MST-03, 2010/2011
Zadania i odpowiedzi, Odp.MST-08
003231 osi 00 szablon test majerska test zadania zamkniete segmenty podzielnosc i wl, Matematyka dla
Zadania i odpowiedzi Odp.MST-07
zadania-dom, zad-dom-3, Analiza Matematyczna
Zadania i odpowiedzi, Odp.MST-04.cd, 2010/2011
Zadania i odpowiedzi, Odp.MST-04, 2010/2011
matma zad, Z3, Zadania z matematyki dla studentów I-go roku studiów stacjonarnych
matma zad, Z17, Zadania z matematyki dla studentów 1 - go roku
matma zad, Z12, Zadania z matematyki dla studentów 1 - go roku
matma zad, Z10, Zadania z matematyki dla studentów I - go roku studiów stacjonarnych
matma zad, Z11, Zadania z matematyki dla studentów I - go roku studiów stacjonarnych
matma zad, Z7(2), Zadania z matematyki dla studentów 1- go roku
matma zad, Z4, Zadania z matematyki dla studentów 1-go roku studiów stacjonarnych
Bukiety matematyczne dla gimnazjum zadania przygotowujące do konkursów
więcej podobnych podstron