Wykład 1 09.10.2002 r
Globalny satelitarny system TRANSIT 1864.
Jego podstawą było 6 satelitów stale okrążających Ziemię. W 1978 r. wystrzelono na orbitę 1 - ego satelitę. W latach 80 - tych udostępniono system dla użytkowników cywilnych.
System odniesienia WGS - 84
Globalny satelitarny system pozycjonowania i nawigacji NAUSTAR GPS ( do określania czasu i odległości ).
System GPS składa się z 28 satelitów poruszających się po orbitach na wysokości ok. 20 000 km ponad powierzchnią Ziemi. Satelity okrążają Ziemię w okresie ok. 11h 57 min na 6 orbitach nachylonych do płaszczyzny równika pod kątem 45° .
Składniki systemu GPS:
Segment satelitarny,
Segment kontrolny - sekcje śledzące,
Segment użytkowników.
Satelita - dwie baterie słoneczne i duży moduł w środku
Najwięcej satelitów nad równikiem. Najmniej nad biegunem.
Stacje kontrolne systemu GPS (5) [ główna Kolorado Spring (Ameryka Północna)]
Zasada wyznaczenia pozycji odbiornika GPS:
Przestrzenne liniowe wcięcie wstecz,
Dane: SV1 (X, Y, Z) ; SV2 (X, Y, Z) ; SV1 (X, Y, Z),
Pomierzone: p1, p2, p3, ..................... , pi ,
Szukane : współrzędne P (X, Y, Z) i = 1,2,3,4,5
Do wyznaczenia współrzędnych przestrzennych - 4 satelity (pozycja 3D).
Dla 3 satelitów - można wyznaczyć pozycje 2D.
Pomiar odległości satelita - odbiornik
Na zasadzie pomiaru czasu jaki zajmuje dotarcie wysłanych przez satelitę wysokiej częstotliwości i niskiej mocy sygnałów radiowych do odbiornika GPS na Ziemi.
Podstawowa częstotliwość: f 0 = 10,23 MHz
Sygnały transmitowane przez satelitę GPS: L1 = 154 f 0 , L2 = 120 f 0. Częstotliwości L1 , L2 są modulowane.
Częstotliwość kodu CIA odpowiada długości fali 293 m o powtarzalności 1 milisekundy.
Kod precyzyjny - długość fali 29,3 m
Ma 10 x większą rozdzielczość
Depesza nawigacyjna (informacje o czasie, systemie, poprawkach zegara)
Zastosowanie technik GPS:
Pomiary satelitarne,
Dynamiczne techniki DGPS i RTK,
?
Wykład 2 16.10.2002 r
Sygnał satelitarny:
Podstawową cechą sygnału GPS jest jego stabilność:
Podstawowe częstotliwości w paśmie L wynoszące f0 = 10,23 MHz na podstawie częstotliwości szacowanej.
Długość fal:
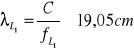
C - prędkość światła w próżni
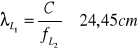
Kod CIA jest kodem cywilnym wykorzystywanym przez najprostsze odbiorniki satelitarne.
Kod P bardziej złożony. Jego rozdzielczość jest 10 razy większa od kodu CIA , λ = 29,31 m .
Kod Y jest wynikiem zaszyfrowania kodu P, jest to kod zaszyfrowany.
Satelita wysyła kody fazowe L1 ( L1 - częstotliwość) kod jest dostępny
Częstotliwość L2
Zastosowanie systemu GPS;
Pomiary statyczne (geodezyjne):
Projektowanie sieci osnów GPS,
Wyznaczanie współrzędnych punktów osnów geodezyjnych,
Transformacje współrzędnych do układów lokalnych,
Modernizacja szczegółowej osnowy geodezyjnej,
Modernizacja ewidencji gruntów.
Dynamiczne technik DGPS i RTK ( odbiornik w ruch ):
Nawigacja pojazdów,
Inwentaryzacja istniejących osnów geodezyjnych,
Wytyczenie tras rurociągu,
Tworzenie numerycznej mapy terenu.
Projekt sieci stacji referencyjnych,
Nawigacja i monitorowanie pojazdów
Nawigacja lądowa:
Nawigacja samochodowa,
Monitorowanie pojazdów policji, straży pożarnej, służby morskiej,
Nawigacja morska:
Pomiary batymetryczne (dno morza, jeziora). W pomiarach batymetrycznych:
dane o pozycji,
dane o głębokości.
Nawigacja powietrzna;
Kontrola toru lotu samolotu.
Poprawka jonosferyczna, troposferyczna - Jks , Tks
Poprawka zegara satelity i odbiornika - dts , dtk
Szumy - ε.
ITRF - International Terrestnal Reference Frame,
ITRS - umowny układ ziemski (od 1991 r.), (wcześniej był CTS),
IERS - International Earth Rotation Sernce
LLR
SLR
VLBI
IGS
geometrii (precyzji i czasu) GDOP
pozycji PDOP
czasu TDOP
błędy wynikające z działania systemu GPS
błędy efemeryd (orbit)
błędy określenia czasu (zegarów) w satelitach i odbiornikach
błędy z powodu geometrycznego wzajemnego ustawienia satelitów (DOP)
błędy wynikające z faktu propagacji sygnału w ośrodku materialnym (nie w próżni), w którym zmianie ulega prędkość rozchodzenia się fali, częstotliwości i polaryzacji sygnału.
refrakcję jonosferyczną
refrakcję troposferyczną
wielotorowość sygnału (multipath)
zmiana parametrów orbit satelitów w depeszy nawigacyjnej, by spowodować pozorną zmianę położenia satelity (
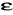
)celowe zaburzenia częstotliwości zegara satelity (dither)
stosować pomiary fazowe do wygładzenia pomiarów kodowych
stosować filtry
stosować anteny - blokują one wpadanie do anteny odbitych fal
wygładzać można przy pomocy fali nośnej (dotyczy sytuacji, gdy odbiornik jest w ruchu)
Wykład 3 23.10.2002 r
Odległość od satelity do punktu K:
![]()
c - prędkość propagacji sygnału.
Błędy:
![]()
Globalne układy odniesienia:
ITRF - jest, co jakiś czas zmieniany (odtwarzany) np.:, co 10 lat brane jest pod uwagę obrót ziemi wokół osi, która się odkształca.
Systemem odniesienia jest środek mas ziemi.
Na całej ziemi jest 70 stacji w Europie 35.
Wprowadzono system ETRF - 89 w 921. ETRF rozszerzono na Polskę (sieć 11 punktów ). EUREF rozszerzone o punkt POLREF tworzy sieć geodezyjną w Polsce. JTRE 89, a nowsza wersja JTRF 96.
Układ WGS - 84 (Globalny system odniesienia).
Układ został ustanowiony przez PMA ( Departament Stanów Zjednoczonych w 1964 r.).
Układ 66, układ 72.
Spójność systemu WGS - 84 i ITRS jest na poziomie 10 cm .
Kontrolowany przez jednostkę NIMA
WGS - 84 - wprowadzono obserwację na 22 punktach obsługujących GPS (od 1997 r.)
Wykład 4 30.10.2002 r
Wyznaczenie współrzędnych punktu z kodowych pomiarów pseudoodległości
![]()
Jeżeli pominiemy wpływ błędów ![]()
z równania, to równanie ma postać
![]()
Lewa strona równania zawiera obserwowaną wartość pseudoodległości ora znaną poprawkę zegara satelity. Po prawej stronie mamy 2 niewiadome, odległość topograficzną oraz poprawkę zegara odbiornika.
![]()
![]()
gdzie:
XS,YS,ZS - współrzędne satelity w chwili emisji sygnału
XK,YK,ZK - nieznane współrzędne anteny odbiornika
Zakładając przybliżone współrzędne odbiornika XK0,YK0,ZK0 jako znane można policzyć przybliżoną wartość ![]()
![]()
(4)
Nieznane współrzędne XK,YK,ZK można zapisać jako
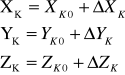
(5)
Funkcję ![]()
można rozwinąć w szereg Taylor'a
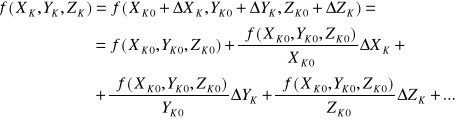
(6)
przy czym równanie to jest skróconym rozwinięciem elementów liniowych
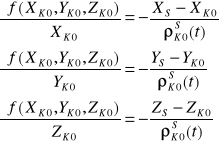
(7)
łącząc równanie (4) oraz (6) i wstawiając (7) otrzymamy równanie liniowe
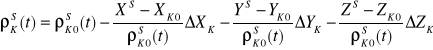
(8)
Wykorzystując (8) liniowe równanie pseudoodległości dla epoki czasu będzie miało postać
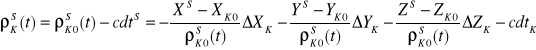
(9)
Wartość poprawki zegara dtS satelity zakłada się jako znaną z depeszy nawigacyjnej. Równanie (9) zawiera 4 niewiadome
![]()
dlatego do rozwiązania nawigacji potrzeba co najmniej 4 satelitów . Wykorzystując powyższe wyrażenia skrótowe
![]()
(10)
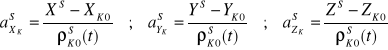
(11)
liniowe równanie pseudoodległości dla n satelitów zapiszemy
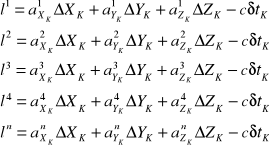
(12)
gdzie indeks górny od 1 do n oznacza numer satelity. Układ równań (12) można zapisać w postaci macierzowej
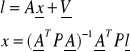
(13)
P - macierz wag
V - macierz poprawek
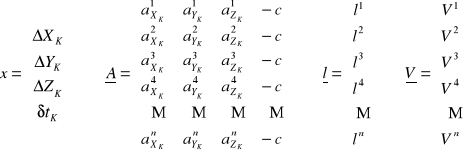
Po uwzględnieniu wprowadzonych oznaczeń (10) i (11) wektor ![]()
oraz macierz ![]()
ma postać
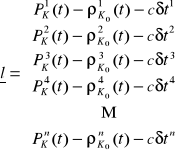
Z liniowego układu równań (13) można wyznaczyć metodą najmniejszych kwadratów różnice współrzędnych
![]()
oraz błąd zegara odbiornika ![]()
na epokę czasu.
Następnie z równania (5) można obliczyć współrzędne obserwowanych punktów, oddzielnie na każdą epokę pomiarową.
Wykład 5 6.11.2002 r
Współczynniki DOP
Dokładność wyznaczeń z pomiarów pseudoodległości jest w głównej mierze uzależniona od geometrii przestrzennej obserwacji konstelacji satelitów względem odbiornika na Ziemi. Geometria ta zmienia się w czasie na skutek ruchu satelitów po orbitach. Trzy pierwsze elementy z każdej kolumny macierzy współczynników ![]()
stanowią wektory jednostkowe pomiędzy punktem obserwowanym na Ziemi , a każdą satelitą.
W wyniku przecięcia się tych wektorów jednostkowych ze strefą (o środku w punkcie obserwowanym) tworzy się bryła geometryczna (wielościan), której odwrotność objętości jest geometrycznym wyznacznikiem rozkładu satelitów w stosunku do odbiornika satelitarnego. Im większa objętość bryły, tym lepsza geometria, a tym samym większa dokładność wyznaczenia współrzędnych odbiornika na Ziemi.
Geometrię rozkładu satelitów określa się za pomocą współczynnika DOP. Są to współczynniki zmniejszenia (rozmycia) precyzji. DOP (Dilution of Precision), które ogólnie można zapisać jako:
![]()
O dokładności precyzji obserwacji możemy mówić po przemnożeniu współczynnika DOP przez dokładności pomiaru.
gdzie:
![]()
- odchylenie standardowe obserwowanej pseudoodległości
![]()
- odchylenie standardowe pozycji np. horyzontalnej lub wertykalnej
Współczynniki DOP są prostymi funkcjami związanymi z elementami diagonalnymi macierzy kofaktorów. Elementami macierzy kofaktorów (QX) są składowe pozycji odbiornika X,Y,Z oraz składowa zegara odbiornika. Zapiszemy ją jako:
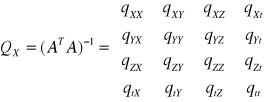
Za pomocą diagonalnych elementów macierzy kofaktorów (QX) zdefiniujemy następujące współczynniki DOP
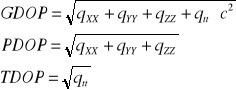
Współczynniki te określają zmniejszenie (rozmycie) precyzji:
Można wyznaczyć rozmycie precyzji dla pozycji horyzontalnej HDOP oraz wertykalnej VDOP w układzie lokalnym. W tym celu macierz QX należy przetransformować do lokalnego układu horyzontalnego otrzymamy macierz kofaktorów dla układu lokalnego:
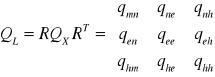
gdzie:
R - macierz rotacji R=[n,e,h]T
n - składowa północna w układzie lokalnym
e - składowa wschodnia w układzie lokalnym
h - składowa wysokościowa w układzie lokalnym
a współczynnik HDOP oraz VDOP zapiszemy jako:
![]()
![]()
Interpretacja geometryczna współczynnika DOP można zapisać jako stosunek:
![]()
Im objętość obserwowanej figury będzie większa tym lepsze geometrie satelitów oraz mniejszy współczynnik DOP satelity.
Interpretacja geometryczna DOP.
Obserwacje fazowe
Obserwacje fazowe stanowią o współcześnie uzyskiwanych wysokich dokładnościach w pomiarach satelitarnych GPS. Obserwacją fazową jest różnica faz fali nośnej sygnału transmitowanego przez satelitę oraz sygnału generowanego przez wewnętrzny oscylator odbiornika. Wynikiem obserwacji jest dokładny pomiar fragmentu długości fali nośnej
L1=19 cm , L2=24 cm
Pomiar zawiera zakumulowaną wartość fragmentu fazy fali nośnej mierzoną od epoki początkowej t0 do danej epoki t oraz nieznaną liczbę początkową, pełnych cykli fali nośnej N. Jest to tzw. nieoznaczoność fazy fali nośnej N (ambiguity). Równanie obserwacji fazy fali nośnej w epoce czasu t z odbiorników k do satelity S ma postać (w cyklach)
![]()
w tym:
![]()
- faza sygnału satelitarnego odebrana z satelity S
![]()
- faza sygnału satelitarnego generowana przez odbiornik K
![]()
- nieznana liczba pełnych okresów fali nośnej w pierwszej epoce czasu tzw. nieoznaczoność fazy fali nośnej
![]()
- szum przypadkowy pomiaru fazy fali nosnej
Powyższe równanie w postaci liniowej po uwzględnieniu poprawki jonosferycznej ![]()
i poprawki troposferycznej ![]()
ma następujący zapis:
![]()
- długość fali
![]()
Wykład 6 13.11.2002 r
Pozycjonowanie względne.
Celem pozycjonowania względnego (różnicowego) jest określenie nieznanych współrzędnych punktu B na podstawie znanych współrzędnych stacji A. Wyznaczeniu podlega zatem wektor zwany linią bazową. Przypisując odpowiednim punktom wektory pozycji odpowiednio ![]()
oraz ![]()
możemy zapisać:
![]()
Z tej zależności wektor linii bazowej będzie określony jako:
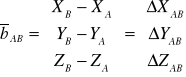
Pozycjonowanie względne jest niezmiernie ważnym elementem w systemie GPS decydującym o wysokiej dokładności pomiarów fazowych oraz kodowych.
Proces ten polega na tworzeniu nowych równań obserwacyjnych poprzez różnicowanie równań obserwacji fazy lub pseudoodległości pozyskanych synchronicznie przez 2 odbiorniki. Postępowanie takie ma na celu eliminację bądź znaczne obniżanie błędów pomiarowych związanych głównie z niedokładnością wzorów czasu i zmiennymi wartościami opóźnień atmosferycznych. W procesie różnicowania obserwacji wyróżniamy tzw. pojedyncze, podwójne i potrójne różnice pomiarów fazowych (kodowych)
Różnica dwóch obserwacji fazowych ( lub kodowych) sygnału emitowanego przez satelitę S, obserwowanego jednocześnie przez odbiorniki k i m wynosi:
![]()
i nosi nazwę pojedynczej różnicowej obserwacji fazowej. Różnicując dwa równania obserwacji fazy typu
![]()
i oznaczając odpowiednie wyrazy różnic przez ∆ otrzymamy:
![]()
Różnica uzyskana pomiędzy dwiema jednoczesnymi pojedynczymi różnicami obserwacji fazowych (lub kodowych) odniesionych do dwóch różnic satelitów S i q nosi nazwę podwójnej różnicowej obserwacji fazowej i wyraża się:
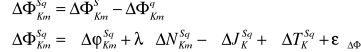
to równanie pozbawione jest błędów zegara satelity i odbiornika.
Dotychczasowe różnicowanie dotyczyło obserwacji wykonywanych jednocześnie w epoce czasu (t). Przez zróżnicowanie podwójnych różnicowych obserwacji dla 2 epok pomiarowych (t1 i t2) możemy wyeliminować niezależne od czasu nieoznaczoności (N). Taką różnicę nazywa się potrójnym różnicowaniem obserwacji fazowej .
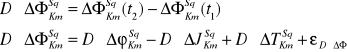
Podstawowe źródła błędów w pomiarach GPS.
Źródłem błędów w pomiarach GPS jest kilka grup czynników:
Występują także błędy powstające w urządzeniach odbiorczych oraz spowodowane celowym wprowadzaniem zakłóceń przez właściciela systemu (np. SA). Do przyczyn błędów niezależnych od zasady działania systemu GPS należy zaliczyć:
Wykład 7 20.11.2002 r
Błędy efemerydalne
Różnice między prawdziwymi, a podawanymi w depeszy nawigacyjnej , położenie satelity na orbicie to błędy wynikające z niedokładności modelu ruchu satelity oraz nieprzewidywalnych perturbacji jego ruchu rzeczywistego . Dane efemerydalne mogą być fałszowane degradacją sygnału SA., co zwiększa błąd położenia satelity na orbicie z kilku do kilkudziesięciu metrów. Orbity satelity są monitorowane naziemnie przez stacje śledzące i poprawiane przez segment kontrolny systemu GPS. Błędy powstają pomiędzy kolejnymi uaktualnieniami pozycji satelitów na orbitach i wzrastają w miarę upływu czasu. Błędy efemerydalne nadawane w czasie rzeczywistym w depeszy nawigacyjnej wynoszą do 21 m
Rodzaj orbit Dokładność czas
Broadcast 3,00 w czasie rzeczywistym
CODE Preclicted 0,20 w czasie rzeczywistym
CODE Rapie 0,10 po 16 godzinach
CODE Final 0,05 po 5-11dniach
IGS Ultra Rapie 0,20 po 3 godzinach
IGS Rapie 0,10 po 19 godzinach
IGS Final 0,05 po 13 dniach
Błędy zegara satelity
Na pokładzie satelity znajdują się atomowe wzorce częstotliwości o wysokiej stabilności krótkoterminowej. Błąd zegara satelitarnego jest spowodowany niedokładną synchronizacją wzorców satelitarnych do czasu GPS. Poprawki zegarów satelitów GPS są wyznaczane przez segment kontrolny na podstawie opracowania danych pochodzących ze stacji śledzących.
Współczynniki wielomianu aproksymującego są retransmitowane przez satelity GPS do użytkowników w depeszy nawigacyjnej. Parametry te umożliwiają obliczenie wartości poprawki zegara satelitarnego z dokładnością do pojedynczych metrów.
![]()
a0,a1,a2 - współczynniki wielomianu transmitowane w depeszy satelitarnej
t - czas, w którym wyznaczana jest poprawka
t0 - epoka poprawki
Bez zakłóceń SA wpływ tego błędu wynosi 1-2 m ( na pomiar pseudoodległości )
SA - Selective Availability - zafałszowanie pozycji satelity jest to tzw. ograniczony dostęp, zakłócenia na sygnał wysyłane przez satelitę. 2 składowe
Efekt dither powodował generator fali nośnej o zmiennej częstotliwości ( zmienna kodu zegara sat.)
Wykład 8 27.11.2002 r
Refrakcja jonosferyczna
Obecność swobodnych elektronów w jonosferze zmienia kierunek i prędkość propagacji sygnału satelitarnego GPS. Wartość zakłóceń zależy od stanu aktywności jonosfery i może wynosić od kilku metrów w okresie niskiej aktywności do 10-20 metrów w czasie jej silnej aktywności. W ciągu dnia szczyt aktywności jonosfery występuje po około 2 godzin od lokalnej kulminacji górnej Słońca.
Poza tym szczególna aktywność może być spowodowana okresowymi burzami słonecznymi i sztormami magnetycznymi. Wpływ na refrakcję jonosferyczną ma także niska wysokość satelity nad horyzontem, a tym samym mały kąt przecinania jonosfery przez sygnał satelitarny.
Stan jonosfery opisuje się za pomocą parametru całkowitej zawartości elektronów TEC (Total Elektron Kontent) mającego największy wpływ na propagację fal radiowych. Parametr TEC wyraża się w jednostkach TECV (jeden TECV odpowiada liczbie 1016 elektronów zawartych w cylindrze o przekroju 1 m2 ustawionym wzdłuż biegu fali radiowej). Zmiany c mogą sięgać w krótkim czasie od -80% do +800% w stosunku do wartości w okresach niezaburzonych.
Opóźnienie sygnału w jonosferze jest wprost proporcjonalne do liczby swobodnych elektronów TEC oraz odwrotnie proporcjonalne do kwadratu częstotliwości fali nośnej :
![]()
gdzie:
c - prędkość światła w próżni
f - częstotliwość sygnału
Wpływ refrakcji jonosferycznej na sygnał satelity jest jednym z najpoważniejszych źródeł błędów wyznaczenia pozycji przy pomocy systemu GPS. Zmiany TEC zmieniają się w cyklach wieloletnich, rocznych i dobowych, ale również przypadkowych.
Refrakcja troposferyczna
Troposfera stanowi niższą część atmosfery i sięga do wysokości ok. 16 km nad powierzchnię równika Ziemi. Na zniekształcenie pomiaru odległości od satelity wpływają zmiany prędkości rozchodzenia się fali elektromagnetycznej. W troposferze na skutek zmian gęstości powietrza, wilgotności, temperatury i ciśnienia. Znaczna część całkowitego opóźnienia ok. 90% jest spowodowane poprzez oddziaływanie fali elektromagnetycznej z suchym powietrzem, zaś pozostałe 10% przez oddziaływanie z parą wodną. Część sucha opóźnienia może być oszacowana z błędem 2-5% za pomocą odpowiedniego modelu atmosfery. Część mokra opóźnienia troposferycznego może być wyznaczone przy pomocy radiometrów mikrofalowych. Niestety jest to bardzo drogie urządzenie i w praktyce błąd „mokrego” opóźnienia jest pomijany. Wartość błędu refrakcji troposferycznej na pomiar pseudoodległości zależy także od kąta wzniesienia satelity nad horyzontem i wynosi do 2-3 m i ok. 20 m dla kąta wzniesienia powyżej 100 w pomiarach GPS można usunąć 90% błędów refrakcji troposferycznej używając modelu uwzględniającego wysokość elewacji satelity.
Efekt MULTIPATH
Efekt wielotorowości sygnału satelity ma miejsce wtedy, kiedy do anteny odbiornika docierają nie tylko sygnały bezpośrednio (najkrótszą drogą), lecz także odbiera od obiektów będących w pobliżu anteny. Fale elektromagnetyczne odbijają się od budynków, konstrukcji metalowych, pojazdów, drzew, lustra wody, gleby. Występują także zjawisko odbijania sygnałów pochodzących z anteny od różnych bliskich obiektów.
Błąd wielotorowości powstaje wtedy, gdy pseudoodległość jest wyznaczana na podstawie sygnałów, które w drodze od satelity do odbiornika uległy odbiciu. Szczególnie duży wpływ na dokładność pomiaru pseudoodległości obserwujemy w pomiarach kodowych. Przeciętnie efekt multipath może powodować błąd pomiaru pseudoodległości w granicach 10-20 m, a w pewnych przypadkach wśród wysokich budynków nawet 100 m.
Wpływ efektu wielotorowości na pomiary satelitarne można określić z pewnym przybliżeniem, wykorzystując dwuczęstotliwościowe obserwacje kodowe i fazowe, lub stosując w odbiorniku często przedziałowy filtr, w układzie opóźnienia kodu. Do wyeliminowania efektów multipath . . . . .
Eliminacja efektów multipath
Wykład 9 04.12.2002 r
Kodowe pomiary DGPS
Metoda lokalnych pomiarów różnicowych DGPS (Differentiall Global Positoining System), wykorzystuje do wyznaczenia pozycji w czasie rzeczywistym, kodowe pomiary pseudoodległości na częstotliwości L1 (C/A). W technice DGPS używa się, co najmniej dwóch odbiorników satelitarnych. Jeden umieszczony jest na punkcie o znanych współrzędnych (precyzyjnie wyznaczanych) i stanowi tzw. stację referencyjną. Drugi ruchomy odbiornik określa pozycję anteny i poprawia ją wykorzystując odebrane ze stacji . . . . . .
Stacja bazowa wykonuje ciągłe obserwacje kodowe, wyznacza swoją pozycję aktualną i określa poprawki korekcyjne do pomierzonej pseudoodległości na zasadzie porównania pozycji aktualnej wyznaczonej ze współrzędnych znanych. Odbiornik na stacji referencyjnej porównuje obliczoną wartość pseudoodległości do poszczególnych satelitów satelitów pseudoodległościami rzeczywistymi, wyznaczonymi na podstawie znanej pozycji stacji. Obliczone poprawki wysyłane są poprzez radiomodem lub telefon komórkowy do odbiornika ruchomego.
W ten sposób pozycja absolutna odbiornika ruchomego jest korygowana poprzez uwzględnienie poprawek wyznaczonych przez stację bazową, eliminując istotne błędy systemu GPS (wpływ jonosfery, troposfery na propagację sygnału radiowego, błąd zegara satelity, błędy efemerydalne, błąd degradacji sygnału satelitarnego S.A.). Stosując technikę DGPS możemy w czasie prawie rzeczywistym wyznaczyć pozycję obiektu ruchomego z dokładnością 0,5-3 m w zależności od klasy sprzętu i warunków satelitarnych w trakcie obserwacji.
Obliczenie poprawki DGPS
Na podstawie porównania rzeczywistej odległości stacji referencyjnej i satelity ![]()
, oraz pseudoodległości ![]()
mierzonej w trakcie obserwacji. Podstawowe równanie obserwacji kodowych ![]()
dla stacji referencyjnej R, uwzględnia także błędy parametrów orbity satelity ![]()
oraz wpływ degradacji sygnału SA ma postać
![]()
Prawdziwą odległość od anteny odbiornika do mierzonego w danej epoce czasu t satelity ![]()
, obliczamy wykorzystując znane współrzędne stacji XR,YR,ZR, oraz współrzędne satelity XS,YS,ZS, obliczone z algorytmu efemerydalnego na podstawie depeszy nawigacyjnej
![]()
Wykorzystując poprzednie wzory możemy obliczyć wartość poprawek korekcyjnych pseudoodległości PRC (Pseudo Range Correction) w epoce czasy t0 dla danego satelity
![]()
Wartość poprawki obliczona w odbiorniku na stacji referencyjnej w czasie t0 w rzeczywistości dociera do odbiornika ruchomego z pewnym opóźnieniem t-t0 (które powinno być uwzględnione). Dlatego stacja referencyjna DGPS oprócz podstawowej wartości poprawki różnicowej PRCS(t0) wysyła również szybkość zmian tej poprawki PRCS(t) (Rate of Pseudo Range Correction)
![]()
Obserwowaną pseudoodległość dla wyznaczanego odbiornika ruchomego M w epoce czasu t możemy zapisać
![]()
Dodając poprawki różnicowe ![]()
otrzymamy
![]()
Wyeliminowane zostały błędy zegara satelity oraz degradacji SA. Błąd jonosfery i troposfery są małe. Ostateczne równanie
![]()
Wyznaczona pozycja
Wyszukiwarka
Podobne podstrony:
Geo fiz wykład 5 03 2013
Geo ściąga 4, Wykład: 07
Geo fiz wykład 9 01 2013
satka(1), geodezja, ROK II, Geo Sat
Geo fiz wykład 12 03 2013
Geo fiz wykład 12 12 2012
Geo sat s
Geo fiz wykład 7 11 2012
Geo fiz wykład 28 11 2012
Program praktyk 2009 v2(1), geodezja, ROK II, Geo Sat
Geo sat, s
Geo fiz wykład 19 03 2013
Geo sat opracowane
Geo fiz wykład 5 03 2013
więcej podobnych podstron