fiz.27, Tomasz Pajączkowski

Tomasz Pajączkowski

19.12.2001

Ćwiczenie nr 27.

Temat: Wyznaczanie maksymalnych prędkości wyjściowych elektronów emitowanych przez termokatodę.

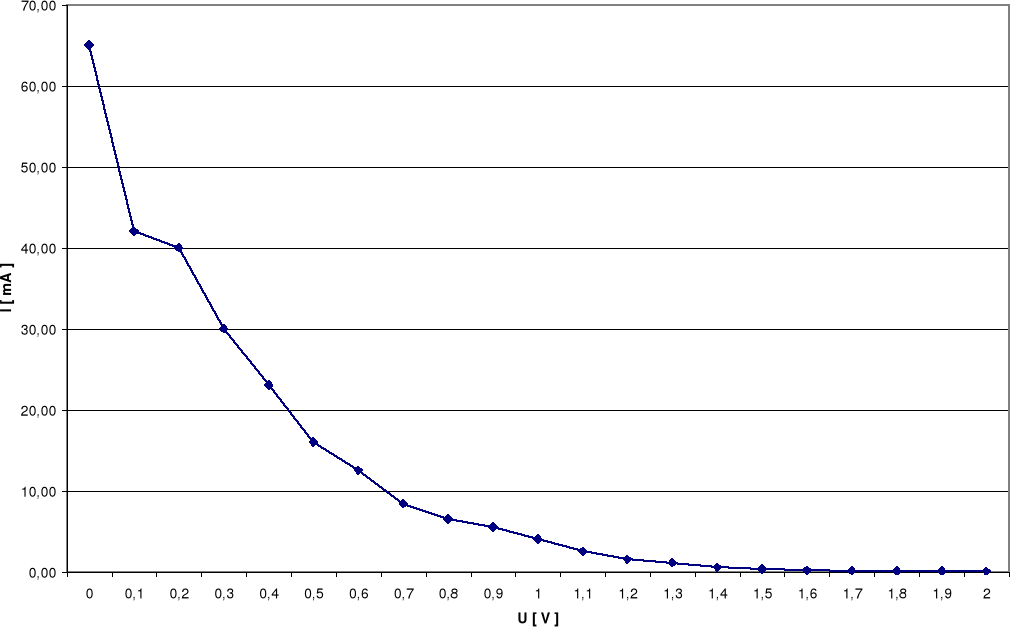
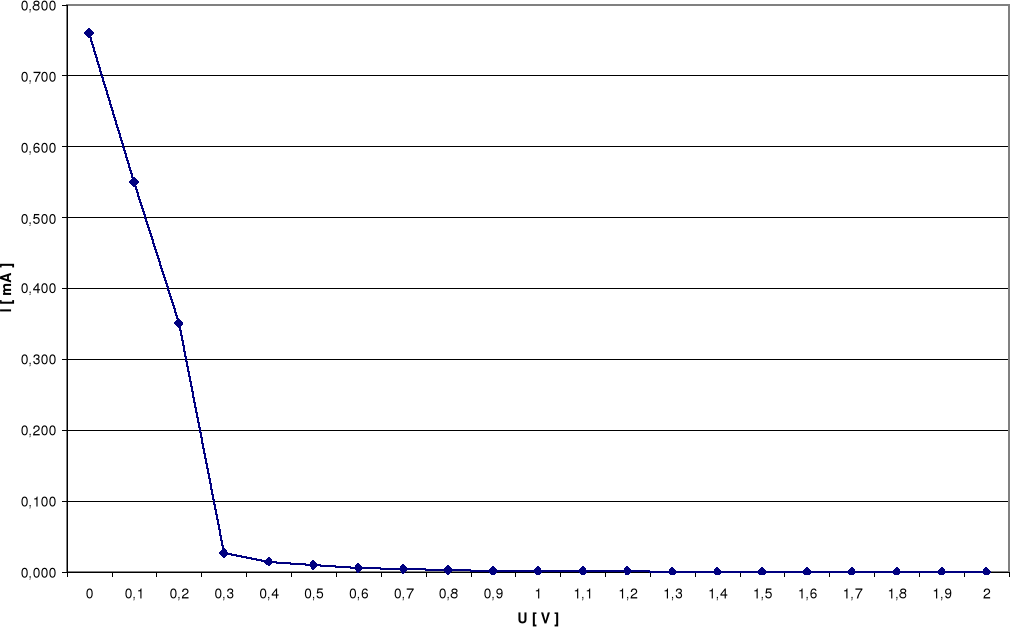
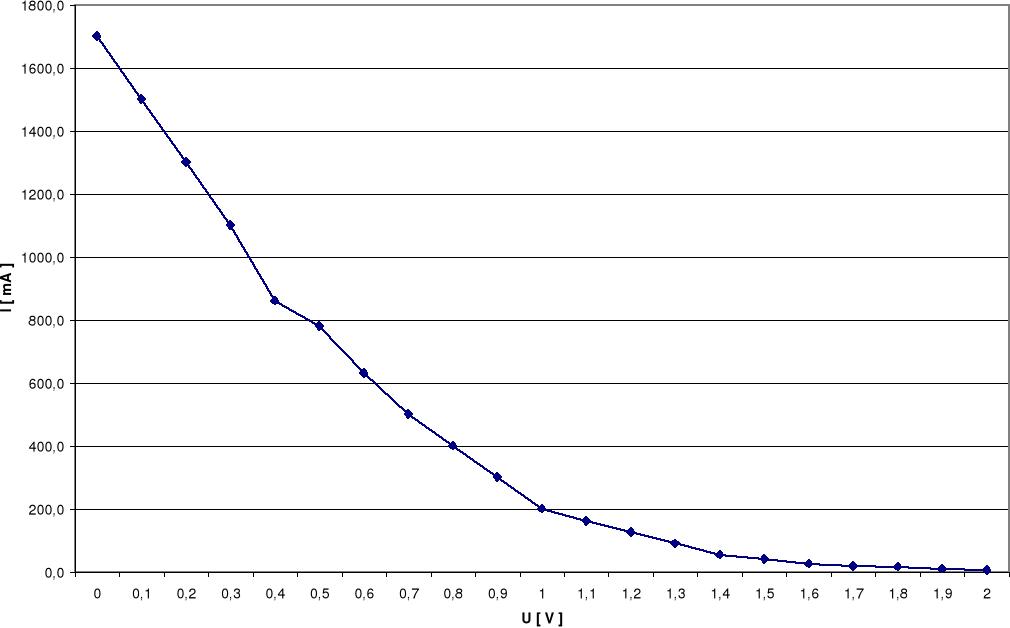
Tabela zebranych wartości:

U [ V ]	I [ mA ]
U [ V ]		dla U_ż= 12V	dla U_ż= 9V	dla U_ż= 6V
0,0	1700,0	65,00	0,760
0,1	1500,0	42,00	0,550
0,2	1300,0	40,00	0,350
0,3	1100,0	30,00	0,026
0,4	860,0	23,00	0,014
0,5	780,0	16,00	0,009
0,6	630,0	12,50	0,005
0,7	500,0	8,40	0,0035
0,8	400,0	6,50	0,002
0,9	300,0	5,50	0,001
1,0	200,0	4,00	0,0006
1,1	160,0	2,50	0,0005
1,2	125,0	1,50	0,0004
1,3	90,0	1,10	0,0
1,4	54,0	0,50	0,0
1,5	40,0	0,32	0,0
1,6	25,0	0,15	0,0
1,7	18,0	0,10	0,0
1,8	16,0	0,06	0,0
1,9	9,0	0,04	0,0
2,0	5,0	0,02	0,0

Teoria zjawiska.

Szereg doświadczeń wykazuje bezpośrednio obecność swobodnych elektronów w metalu. Klasyczna teoria przewodnictwa metali opracowana przez P.Drudego w 1900r. opiera się właśnie na założeniu, że nośnikami prądu w metalach są elektrony poruszające się w sieci krystalicznej dodatnich jonów. Duża koncentracja elektronów oraz chaotyczny ruch cieplny elektronów pozwoliły zastosować dla elektronów podobne związki jak dla gazu doskonałego. Mówi się nawet o gazie elektronowym. Podobnie jak cząsteczki cieczy odrywają się od jej powierzchni w zjawisku parowania, tak i swobodne elektrony mogą wydostać się na zewnątrz metalu. Metal opuszczają tylko te elektrony, których energia kinetyczna będzie większa od minimalnej wartości energii, zwanej praca wyjścia. Liczba emitowanych elektronów rośnie ze wzrostem temperatury. Zjawisko opuszczania metali przez elektrony pod wpływem wysokiej temperatury nazywamy termoemisją. Emisje elektronów można wywołać również innymi czynnikami, takimi jak: oświetleniem, przyłożonym pole elektryczne, bombardowaniem powierzchni metalu cząstkami itp.

Lampa elektronowa należy do przyrządów, których działanie polega na przepływie strumienia elektronów między elektrodami umieszczonymi w bańce próżniowej. Źródłem elektronów jest żarzona elektrycznie katoda. Katoda żarzy się pod wpływem płynącego prądu i takie żarzenie nazywamy bezpośrednim. W klasycznej próżniowej lampie dwuelektrodowej ( diodzie ) katoda wykonana jest z czystego wolframu - odznaczającego się wysoką zdolnością emisyjną w wysokiej temperaturze. Zjawisko to zwane termoemisją lub zjawiskiem Richardsona opisane zostało powyżej. Wyemitowane z katody elektrony tworzą wokół niej pewien ładunek przestrzenny zwany chmurą elektronową. Elektrony te poruszają się w polu elektrycznym wytworzonym pomiędzy elektrodami lampy. Elektrony opuszczające powierzchnię katody posiadają pewną prędkość, zwaną prędkością wyjścia. Prędkości wyjścia dla poszczególnych elektronów są różne, a ich rozrzut pokrywa się z rozkładem prędkości Maxwella.

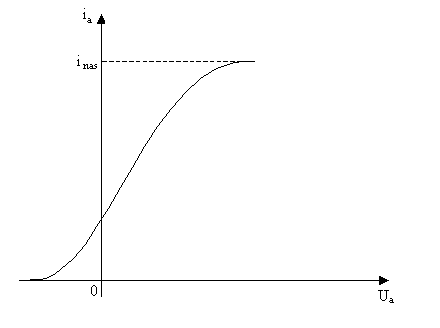
0x08 graphic
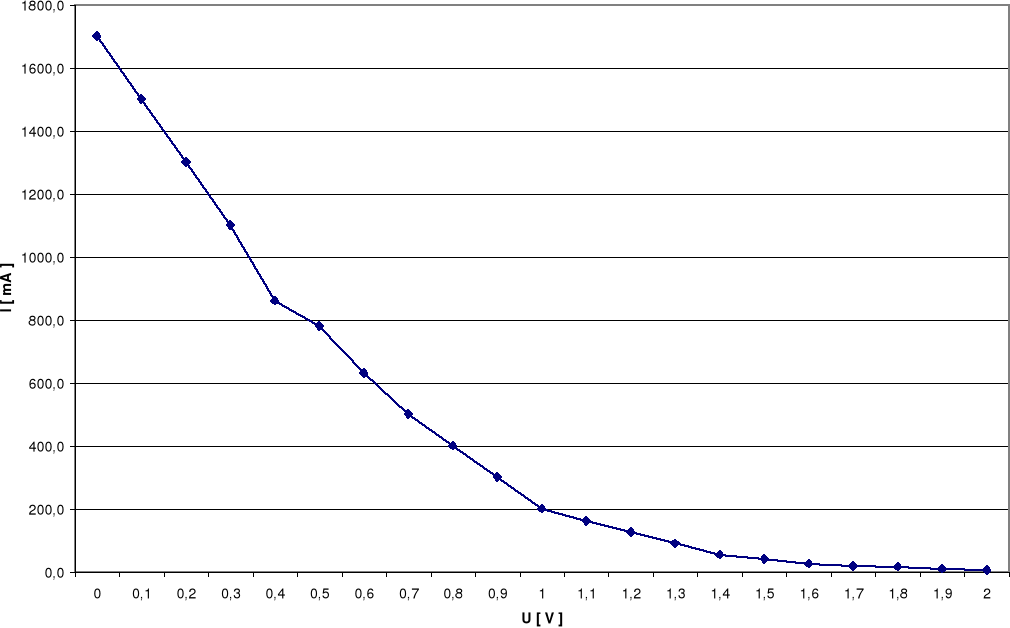
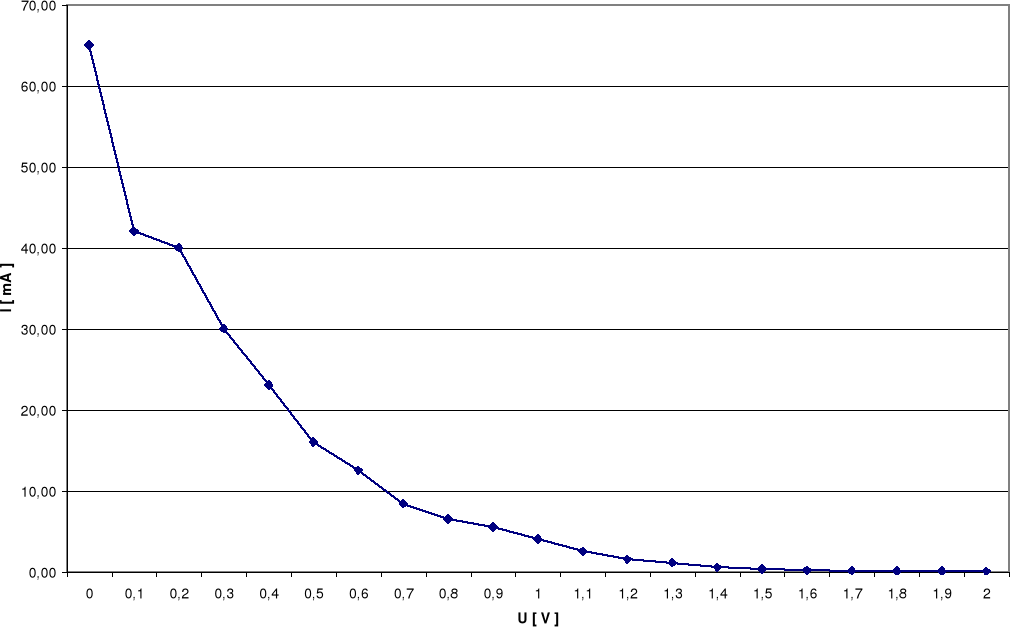
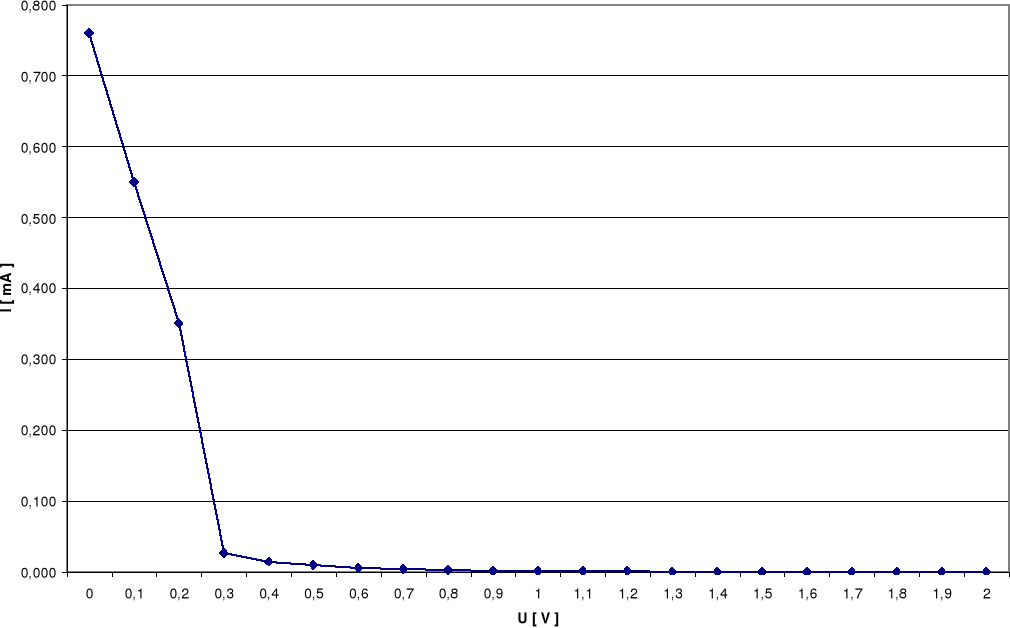
Dla takiej lampy charakterystyka prądowo - napięciowa ma przebieg pokazany na poniższym wykresie.

Powyższy wykres charakteryzuje się dwiema osobliwościami:

w zakresie małych napięć natężenie prądu proporcjonalne jest do napięcia w potędze 3/2, co wykazał Langmuir i_a = BU^3/2
dla dużych napięć natężenie prądu anodowego praktycznie nie zależy od napięcia, a stan taki nazywamy nasyceniem. Nasycenie prądu anodowego wykazują jedynie diody żarzone bezpośrednio, z katodami wolframowymi, nie aktywowanymi.

Stosując dla gazu elektronowego prawo rozkładu prędkości Maxwella:

dN/N = ( 4/√π )·( m/2kT )^3/2·v² exp( -mv²/2kT )dv

gdzie: k - stała Boltzmanna, m - masa elektronu, T - temperatura bezwzględna, określić możemy gęstość prądu anodowego w zakresie nasycenia następującym wzorem:

j_nas = CT^1/2 exp( -W/kT )

gdzie: gęstość prądu j = ia/S, W - praca wyjścia elektronu z metalu, S - pole przekroju strumienia elektronów (pole powierzchni katody ), C - stała zależna od rodzaju metalu:

C = n( k/2πm )^1/2

gdzie: n - koncentracja elektronów.

Dushman posługując się kwantową teorią metali na drodze termodynamicznej wykazał, że gęstość prądu nasycenia określona jest wzorem:

j_nas = AT^1/2 exp( -W/kT )

gdzie: A = 2πmek²/h³ = 60,2 A/cm²K²; h - stała Plancka.

Przy przyjęciu rozkładu Fermiego otrzymuje się podobną zależność:

j_nas = BT^1/2 exp( -W/kT )

gdzie: B = c·A/2; c - średnia wartość tzw. współczynnika przepuszczalności bariery potencjału na powierzchni metalu.

Jeśli przyjmiemy, że szerokość wiązki elektronowej prądu anodowego nie zależy od temperatury, to powyższe równanie możemy przekształcić do postaci:

i_nas = SBT^1/2 exp( -W/kT )

Wyprowadzenie wzoru roboczego:

Elektrony przebywające różnicę potencjałów U muszą wykonać pracę równą: L = eU. Pracę tę wykonują kosztem energii kinetycznej E_k = mV²/2.

Do anody mogą dojść tylko elektrony o dostatecznie dużej energii, przekraczającej pracę przeciw potencjałowi hamowania. mV²/2 ≥ eU_m gdzie: e - nabój elektronów, U_m - potencjał hamujący.

Ze wzrostem ujemnego potencjału anody liczba elektronów o energii wystarczającej do pokonania potencjału hamującego anody, jest coraz mniejsza i prąd w obwodzie anodowym maleje. Przy pewnej wartości U = U_m żaden z elektronów nie dochodzi do anody, przyczym spełniony jest warunek: mV²_max/2 = eU_m, a stąd maksymalna prędkość elektronów wyraża się zależnością: V_max = √(2eU_m/m).

Sposób wykonania ćwiczenia.

Celem powyższego ćwiczenia było wyznaczanie maksymalnych prędkości wyjściowych elektronów emitowanych przez termokatodę.

Całkowity pomiar polegał na wyznaczeniu natężenia płynącego prądu w układzie dla zmieniającego się napięcia hamowania od 0V do 2V ( przy czym napięcie to zmieniało się co 0,1V ). Pomiarów tych dokonać należało przy napięciu w układzie włókna grzejnego katody 12V, 9V i 6V, co też uczyniłem.

Uzyskane w ten sposób wartości zebrałem w powyższej tabeli, a następnie na ich podstawie wykreśliłem dołączone wykresy, dokonałem poniższych obliczeń i wyciągnąłem końcowe wnioski.