Wybrane zadania do ćwiczeń ze statystyki, 3 sem. Wydziału Chemicznego

Zmienne losowe typu skokowego - podstawowe własności

1. Urządzenie składa się z 3 elementów. W ciągu ustalonego czasu T (np. w ciągu jednego roku)

pierwszy element psuje się z prawdopodobieństwem 0,2 ;

drugi - z prawdopodobieństwem 0,3 ;

trzeci - z prawdopodobieństwem 0,4 .

Elementy psują się niezależnie od siebie. Niech X - ilość elementów, które zepsują się w ciągu ustalonego czasu T. Znaleźć rozkład zmiennej losowej X i jej wartość oczekiwaną; wyjaśnić otrzymany wynik.

Rozw. P(X=0) = 0,2*0,3*0,4 = 0,336;

P(X=1) = 0,2*0,7*0,6 + 0,8*0,3*0,6 + 0,8*0,7*0,4 = 0,084+0,144+0,224 = 0,452 ;

P(X=2) = 0,2*0,3*0,6 + 0,2*0,7*0,4 + 0,8*0,3*0,4 = 0,036+0,056+0,096 = 0,188 ;

P(X=3) = 0,2*0,3*0,4 = 0,024 .

Uwaga. EX=0,9 (dokładnie; = 0,2+0,3+0,4; dlaczego? Bo X = X₁+X₂+X₃, gdzie X_i=1, jeżeli i-ty element się zepsuje w ciągu czasu T, 0 - w przeciwnym przypadku).

2. Rzucamy n=5 razy symetryczną monetą. (n=5, p=0,5=q .) Znaleźć rozkład zmiennej losowej X, gdzie X - ilość wystąpień orła w tych rzutach. Odp.: 1/32; 5/32; 10/32; 10/32; 5/32; 1/32. EX=2,5 (=np).

3. To samo dla n=4, p=0,4 (q=0,6).

Rozw.

P(X=0) = 1 * 1 * 0,1296 = 0,1296 ;

P(X=1) = 4 * 0,4 * 0,216 = 0,3456 ;

P(X=2) = 6 * 0,16 * 0,36 = 0,3456 ;

P(X=3) = 4 * 0,064 * 0,6 = 0,1536 ;

P(X=4) = 1 * 0,0256 * 1 = 0,0256 ;

---------

(Razem:) 1,0000 .

4. W partii składającej się z 6 detali znajdują się dwa detale standardowe (spełniające normę).

Losowo wybrano z tej partii 3 detale. Niech X - liczba standardowych detali wśród tych trzech wybranych. Znaleźć rozkład zmiennej losowej X, jej wartość oczekiwaną i wariancję. Naszkicować dystrybuantę.

P(X=0)=0;

P(X=1)= 4/20=1/5 ;

P(X=2)=12/20=3/5 ;

P(X=3)= 4/20=1/5

EX=2; E(X²)=22/5; D²X=2/5 .

5. Dany jest rozkład zmiennej losowej X:

xi	-1	0	1	2	3
pi	0,1	0,3	0,2	0,25	0,15

Znaleźć wartość oczekiwaną i wariancję zmiennej losowej Y=5-2X² , w miarę możliwości dwoma sposobami. (Odp.: EY = -0,3; D²Y = 37,71)

6. Wykazać, że suma dwóch niezależnych zmiennych o rozkładzie Poissona z parametrami λ₁ i λ₂ odpowiednio ma również rozkład Poissona z parametrem λ = λ₁ + λ₂.

Zmienne losowe typu ciągłego - podstawowe własności

1. Dana jest funkcja f(x)=0 dla x<0, f(x)=Ce^-ax dla xł0 (a>0 - ustalone) (wariant: Cxe^-ax).

a) Dobrać C takie, aby funkcja f była gęstością pewnej zmiennej losowej X;

b) Znaleźć dystrybuantę F (=F_X) zmiennej losowej X;

c) Przekonać się, że pochodną otrzymanej dystrybuanty jest gęstość (jest tak zawsze w punktach ciągłości gęstości f(x));

d) Znaleźć P(X<1), P(1≤X<2), P(X≥2) i zinterpretować te prawdopodobieństwa na wykresie

ca) gęstości; cb) dystrybuanty

e) Znaleźć wartość oczekiwaną zmiennej losowej X;

f) Znaleźć, w ogólnym przypadku, związek pomiędzy dystrybuantą F_X zmiennej losowej X a dystrybuantą F_Y zmiennej losowej Y=X²;

g) Mając konkretną postać dystrybuanty F_X, znaleźć dystrybuantę F_Y zmiennej losowej Y=X²;

h) Przez różniczkowanie dystrybuanty znalezionej w poprzednim punkcie, znaleźć gęstość zmiennej losowej Y;

i) Zakładając, że zmienna X jest typu ciągłego, różniczkując związek znaleziony w punkcie g), otrzymać ogólnie związek pomiędzy gęstością f_X zmiennej losowej X a gęstością f_Y zmiennej losowej Y=X²;

j) Zastosować to w konkretnym przypadku, gdy gęstość zmiennej losowej X jest taka jak dana na początku zadania; porównać wyniki otrzymane w tym punkcie z wynikiem otrzymanym w punkcie h);

k) Policzyć dwoma sposobami E(X²):

ka) na podstawie wzoru

;

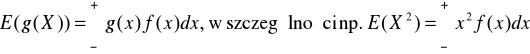
kb) (nie dotyczy) korzystając ze znalezionej gęstości zmiennej Y=X².

2. Dla jakich wartości parametrów a, b funkcja F(x)=0 dla xŁ-c; F(x)=a+b arc sin (x/c) dla -c<xŁc; F(x)=1 dla xłc jest

a) dystrybuantą pewnej zmiennej losowej X;

b) dystrybuantą pewnej zmiennej losowej X typu ciągłego; w tym przypadku znaleźć gęstość zm. los. X;

c) dystrybuantą pewnej zmiennej losowej X typu skokowego.

3. Dystrybuanta zmiennej losowej X ma postać:

F(x) = a dla xŁ-2; F(x) = bx+c dla -2<xŁ2; F(x) = d dla x>2. Wiedząc, że X jest typu ciągłego, znaleźć

a) parametry a, b, c, d; b) gęstość zmiennej losowej X; c) wartość oczekiwaną tej zmiennej; d) E(X²);

e) dystrybuantę zmiennej losowej X² (wariant: Z=4-X²);

f) gęstość zmiennej losowej Y=X² (wariant: Z=4-X²), w miarę możliwości dwoma sposobami.

4. Dana jest funkcja f(x)=C(x-2)(4-x) dla x pomiędzy pierwiastkami tego trójmianu kwadratowego, f(x)=0 dla pozostałych X. a) Dobrać stałą C tak, aby funkcja f była gęstością pewnej zmiennej losowej X; b) Obliczyć EX i D²X. Odp. C=3/4, EX=3 (zwrócić uwagę na symetrię);

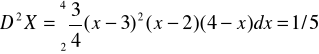
lub D²X=E(X²)-(EX)², gdzie

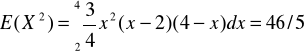
, zatem D²X=46/5-9=46/5-45/5=1/5 .

5. Zmienna losowa X ma rozkład jednostajny (równomierny, prostokątny) na przedziale (0; 1). Znaleźć wartość oczekiwaną i wariancję zmiennej losowej Y=4X³ (w miarę możliwości dwoma sposobami).

Odp.: EY=1; D²Y=9/7.

6. Zmienna losowa X ma dystrybuantę F_X [i ewentualnie gęstość f_X (=F_X'), w przypadku, gdy jest to zmienna losowa typu ciągłego]. Znaleźć dystrybuantę zmiennej Y=1/X [i ewentualnie gęstość Y w przypadku gdy X, a co za tym idzie - Y, jest typu ciągłego], przy czym w ogólnym przypadku zakładamy, że P(X=0)=0 - dzięki czemu 1/X ma (z prawdopodobieństwem 1) sens; w przypadku zmiennej losowej typu ciągłego to założenie jest spełnione automatycznie.

7. Dana jest funkcja: f(x)=0 dla |x|<1; f(x)=C/x⁴ dla |x|ł1 (wariant: f(x)=0 dla x<1; f(x)=C/x⁴ dla xł1).

a) Dobrać stałą C tak, aby funkcja f była gęstością pewnej zmiennej losowej X;

b) Znaleźć dystrybuantę zmiennej losowej X;

c) Znaleźć wartość oczekiwaną i wariancję zmiennej losowej X;

d) Znaleźć gęstość zmiennej losowej Y=X² (wariant: Y=4-X²).

8. Niech F₁ i F₂ będą dwiema dystrybuantami zmiennych losowych X₁ i X₂ odpowiednio. Jeżeli a,b>0 i a+b=1 wykazać, że funkcja F(x)=aF₁(x)+bF₂(x) ma wszystkie własności dystrybuanty.

9. Wyrazić moment centralny 4 rzędu, m₄ przez momenty zwykłe do czwartego rzędu włącznie (m₁, m₂, m₃, m₄. (Zadanie stosuje się do zmiennych dowolnego typu).

10. Niech zmienna losowa X ma rozkład typu ciągłego o ściśle rosnącej dystrybuancie F_X - tak że istnieje funkcja odwrotna do F_X - powiedzmy (F_X)^-1 określona na przedziale (0 ; 1). Wykazać, że rozkład zmiennej Y=F_X(X) nie zależy od rozkładu X spełniającego te warunki - i znaleźć ten rozkład (jego dystrybuantę lub gęstość) - jak się nazywa ów rozkład?

11. Dana jest funkcja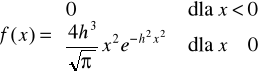
, gdzie h jest pewnym dodatnim parametrem.

a) Wykazać że funkcja f jest gęstością pewnej zmiennej losowej X. (Wsk.: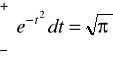
.)

b) Znaleźć E(X),V(X). Odp.: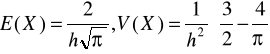
.

12. Obliczyć wartość oczekiwaną i wariancję zmiennej o rozkładzie jednostajnym (czyli prostokątnym) na przedziale
.

Przybliżenie rozkładu Bernoulliego rozkładem Poissona

1. Przy masowych prześwietleniach małoobrazkowych prawdopodobieństwo trafienia na człowieka chorego na gruźlicę jest równe p=0,01. Prześwietlono n=200 osób. Niech X - ilość chorych na gruźlicę wśród tych n przebadanych. Napisać dokładne wzory, wynikające z rozkładu dwumianowego, oraz obliczyć przybliżone wartości wynikające z przybliżenia rozkładu dwumianowego rozkładem Poissona, dla prawdopodobieństw następujących zdarzeń:

a) X=0; b) X=1; c) X=2; d) Xł3.

2. W skład złożonej aparatury wchodzi między innymi 500 elementów określonego rodzaju. Prawdo­podobieństwo uszkodzenia w ciągu roku wynosi dla każdego z tych elementów 0,002 i nie zależy od stanu pozostałych elementów. Podać dokładne wzory na prawdopodobieństwo

a) uszkodzenia w ciągu roku dokładnie jednego elementu

b) uszkodzenia w ciągu roku nie mniej niż jednego elementu

- oraz podać wzory i obliczyć przybliżenia tych prawdopodobieństw, wynikające z przybliżenia rozkładu dwumianowego przez rozkład Poissona.

Rozkłady dwuwymiarowe

1. Rozkład dwuwymiarowy zmiennych X, Y (typu skokowego). Rozkłady brzegowe. Niezależność zmiennych losowych. Ilustracja rozkładu zmiennej X+Y (zależy nie tylko od rozkładów brzegowych). Własności E(X+Y), ew. przygotowanie do wzoru na D²(X+Y). Liczenie np. E(XY) dwoma sposobami. Niezależność zmiennych losowych. Może - kowariancja, współczynnik korelacji.

Przeliczyć, że dla niezależnych zmiennych losowych X, Y mamy E(XY)=(EX)(EY). [Nie zrobiono.]

2. Dany jest rozkład dwuwymiarowy zmiennych losowych X,Y:

yj \ xi	0	1
-1	0,10	0,15
0	0,15	0,25
1	0,20	0,15

a) Znaleźć rozkład zmiennych losowych X i Y (tzw. rozkłady brzegowe);

b) Czy zmienne X i Y są niezależne?

c) Znaleźć rozkład zmiennych X+Y, XY, X², Y², wreszcie Z=3X+Y²;

d) Znaleźć EX, EY, E(X+Y) (dwoma sposobami) E(X²), E(Y²), E(XY) (dwoma sposobami), EZ

e) Znaleźć wariancję zmiennych X, Y, Z.

3) Znaleźć współczynnik korelacji
.

Częściowa odpowiedź: Rozkład X:

xi	0	1
pi	0,45	0,55

Taki sam jest rozkład X²; EX=0,55; EX²=0,55

Rozkład Y:

yi	-1	0	1
pi	0,25	0,40	0,35

EY=0,10, E(Y²)=0,6;

Rozkład X+Y:

ui	-1	0	1	2
pi	0,1	0,3	0,45	0,15

E(X+Y)=EX+EY=0,65 lub E(X+Y)=-1*0,1+1*0,45+2*0,15=-0,1+0,45+0,3=0,65;

Rozkład XY:

vi	-1	0	1
pi	0,15	0,70	0,15

E(XY)=-1*0,15+1*0,15=0 lub
=0

Rozkład Z:

zi	0	1	3	4
pi	0,15	0,3	0,25	0,30

EZ=3EX+E(Y²) = 3*0,55 + 0,6 = 2,25 lub
; D²Z = E(Z²) - (EZ)² = 1*0,3 + 9*0,25 + 16*0,3 -2,25² = 7,35 - 5,0625 = 2,2875 » 2,29

2. Rzucono 5 razy symetryczną monetą. Niech X - ilość wyrzuconych orłów, Y - ilość serii orłów, Z - długość najdłuższej serii orłów. Wypisać wszystkie zdarzenia elementarne w tym doświadczeniu, a następnie wyznaczyć:

a) rozkład zmiennej losowej (X,Y); b) rozkłady brzegowe zmiennych X,Y oraz i wartości oczekiwane;

c) rozkład Z i jej wartość oczekiwaną; d) rozkład (X,Z) oraz P(X=3,Z≤2).

Rozwiązanie: w poniższym zestawieniu 0 oznacza orła, 1 - reszkę.

wynik	X	Y	Z	wynik	X	Y	Z	wynik	X	Y	Z	wynik	X	Y	Z
00000	5	1	5	01000	4	2	3	10000	4	1	4	11000	3	1	3
00001	4	1	4	01001	3	2	2	10001	3	1	3	11001	2	2	2
00010	4	2	3	01010	3	3	1	10010	3	2	2	11010	2	2	1
00011	3	1	3	01011	2	2	1	10011	2	1	2	11011	1	1	1
00100	4	2	2	01100	3	2	2	10100	3	2	2	11100	2	2	2
00101	3	2	2	01101	2	2	1	10101	2	2	1	11101	1	1	1
00110	3	2	2	01110	2	2	1	10110	2	2	1	11110	1	1	1
00111	2	1	2	01111	1	1	1	10111	1	1	1	11111	0	0	0

X Y	0	1	2	3
0	1/32	0	0	0	1/32
1	0	5/32	0	0	5/32
2	0	4/32	6/32	0	10/32
3	0	3/32	6/32	1/32	10/32
4	0	2/32	3/32	0	5/32
5	0	1/32	0	0	1/32
	1/32	15/32	15/32	1/32	1

X Z	0	1	2	3	4	5
0	1/32	0	0	0	0	0	1/32
1	0	5/32	0	0	0	0	5/32
2	0	6/32	4/32	0	0	0	10/32
3	0	1/32	6/32	3/32	0	0	10/32
4	0	0	1/32	2/32	2/32	0	5/32
5	0	0	0	0	0	1/32	1/32
	1/32	12/32	11/32	5/32	2/32	1/32	1

EX=np=5⋅0,5=2,5; EY=1,5 (symetria względem 1,5); EZ=62/32, P(X=3, Z≤2)=7/32.

3. Rzucamy dwa razy rzetelną kostką. Niech U - suma oczek otrzymanych w tych dwóch rzutach, V - wartość bezwzględna różnicy oczek. Znaleźć łączny rozkład dwuwymiarowej zmiennej losowej (U,V); ewentualnie, dla uproszczenia, zamiast rzutu kostką rozważyć eksperyment, w którym można otrzymać wyniki 1,2,3 z jednakowym prawdopodobieństwem. Rozwiązanie (zagadnienia uproszczonego): W tabelce podano rozkład (X,Y) (X - u góry, Y z lewej) wraz z wartościami przyjmowanymi odpowiednio przez (U,V):

yj \ xi	1	2	3
1	1/9 (2,0)	1/9 (3,1)	1/9 (4,2)	1/3
2	1/9 (3,1)	1/9 (4,0)	1/9 (5,1)	1/3
3	1/9 (4,2)	1/9 (5,1)	1/9 (6,0)	1/3
	1/3	1/3	1/3	1/3

Stąd z łatwością otrzymujemy tabelkę rozkładu dla (U,V) (U - u góry, V - z lewej):

vj \ ui	2	3	4	5	6
0	1/9	0	1/9	0	1/9	3/9
1	0	2/9	0	2/9	0	4/9
2	0	0	2/9	0	0	2/9
	1/9	2/9	3/9	2/9	1/9	9/9

Rozwiązanie zagadnienia pełnego, z dwiema kostkami): W tabelce podano rozkład (X,Y) (X - u góry, Y z lewej) wraz z wartościami przyjmowanymi odpowiednio przez (U,V):

yj \ xi	1	2	3	4	5	6
1	1/36 (2,0)	1/36 (3,1)	1/36 (4,2)	1/36 (5,3)	1/36 (6,4)	1/36 (7,5)	1/6
2	1/36 (3,1)	1/36 (4,0)	1/36 (5,1)	1/36 (6,2)	1/36 (7,3)	1/36 (8,4)	1/6
3	1/9 (4,2)	1/9 (5,1)	1/36 (6,0)	1/36 (7,1)	1/36 (8,2)	1/36 (9,3)	1/6
4	1/36 (5,3)	1/36 (6,2)	1/36 (7,1)	1/36 (8,0)	1/36 (9,1)	1/36 (10,2)	1/6
5	1/36 (6,4)	1/36 (7,3)	1/36 (8,2)	1/36 (9,1)	1/36 (10,0)	1/36 (11,1)	1/6
6	1/36 (7,5)	1/36 (8,4)	1/36 (9,3)	1/36 (10,2)	1/36 (11,1)	1/36 (12,0)	1/6
	1/6	1/6	1/6	1/6	1/6	1/6	1

Stąd z łatwością otrzymujemy tabelkę rozkładu dla (U,V) (U - u góry, V - z lewej):

vj \ ui	2	3	4	5	6	7	8	9	10	11	12
0	1/36	0	1/36	0	1/36	0	1/36	0	1/36	0	1/36	6/36
1	0	2/36	0	2/36	0	2/36	0	2/36	0	2/36	0	10/36
2	0	0	2/36	0	2/36	0	2/36	0	2/36	0	0	8/36
3	0	0	0	2/36	0	2/36	0	2/36	0	0	0	6/36
4	0	0	0	0	2/36	0	2/36	0	0	0	0	4/36
5	0	0	0	0	0	2/36	0	0	0	0	0	2/36
	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36	1

4. Przykład. Niech zmienna losowa X ma rozkład jak w poniższej tabelce; zmienne losowe X i Y=X², są oczywiście zależne (bo jedna jest funkcją drugiej; uzasadnić ...); sprawdzić, że mimo to dla X i Y zachodzi równość D²(X+Y)= D²X + D²Y:

xi	-2	-1	1	2
pi	0,25	0,25	0,25	0,25

Rozkład normalny - korzystanie z tablic rozkładu normalnego

1. Wytrzymałość lin z masowej produkcji ma w przybliżeniu rozkład normalny N(1000 kG/cm², 50 kG/cm²). a) Ile przeciętnie lin spośród 1000 ma wytrzymałość mniejszą niż 900 kG/cm²?

b) Co która przeciętnie lina ma wytrzymałość mniejszą niż 900 kG/cm²?

2. Zmienna losowa X~N(3,4). Obliczyć prawdopodobieństwo, że 1≤X²≤9.

3. Wykazać, że jeżeli zmienna losowa X ma rozkład N(m,σ), to zmienna (X-m)/σ ma rozkład normalny N(0,1). (trochę teoretyczne - być może było na wykładzie; w każdym razie musiało zostać sformułowane na wykładzie).)

4. (trudniejsze) Obliczyć czwarty (ew. dalsze parzyste) moment centralny w rozkładzie normalnym

N(m,s) (momenty nieparzystego rzędu są równe zeru) oraz ew. E[|X-EX|^k] dla k nieparzystych (indukcja).

Centralne twierdzenie graniczne

1. Pewne doświadczenie udaje się z prawdopodobieństwem p=0,2 .

a) Przeprowadzono n=50 takich doświadczeń (doświadczenia udają się niezależnie od siebie). Jakie jest prawdopodobieństwo, że ilość udanych doświadczeń będzie się zawierała w przedziale

aa) <5,15>; ab) <15,20> ?

b) Jakie jest prawdopodobieństwo, że częstość udawania się doświadczeń (tzn. stosunek ilości X udanych doświadczeń do n - ogólnej ilości doświadczeń) będzie się różniła od 0,2 co do modułu

ba) o mniej niż ε=0,05 (tzn. będzie się zawierała w przedziale (0,15;0,25) ?

bb) mniej niż o ε=0,01 (tzn. będzie się zawierała w przedziale (0,19;0,21) ?

c) Ile należy przeprowadzić takich doświadczeń, aby z prawdopodobieństwem 0,8 co najmniej 10 doświadczeń było udanych? (Odp. n>=(7,96)², tzn. n=64).

d) Ile należy przeprowadzić takich doświadczeń, aby z prawdopodobieństwem 0,8 częstość udawania się dośw. zawierała się w przedziale (0,18; 0,22)? (Odp: n^1/2/20=1,28; n^1/2=25,6; n>=655,36, czyli 656.)

e) (Dość trudne rachunkowo, chodzi jedynie o ilustrację, że centralne twierdzenie graniczne można wykorzystać do obliczenia dowolnego z parametrów rozkładu.) Ile co najmniej powinno wynosić prawdopodobieństwo p udawania się pojedynczego doświadczenia, aby przeprowadzenie 100 doświadczeń gwarantowało, że z prawdopodobieństwem 0,9 otrzymamy co najmniej 20 udanych doświadczeń?

Rozw. P(X≥20)=0,9; P((X-np)/(npq)^1/2≥(20-100p)/(100p(1-p))^1/2)=0,9; (20-100p)/(100p(1-p))^1/2=-1,28;

400-4000p+10000p²=163,84(p-p²); 10163,84p²-4163,84p+400=0; Δ=17337563,55-4*400*10163,84=

17337563,55-16262144=1075419,55; Δ^1/2=1037,0243; p₁=3126,82/20327,68=0,154 - odrzucamy, bo

20-100p₁>0 [jest to pierwiastek równania (20-100p)/(100p(1-p))^1/2=+1,28]; p₂=52000,86/20327,68 = 0,256. Odp: p≥0,256.

2. Zmienne losowe X₁, X₂, X₃, ..., X₁₀₀ są niezależne, o jednakowym rozkładzie w którym

P(X=k)=2^ke^-2/(k!). Niech X= X₁+ X₂ + ... + X₁₀₀. Obliczyć prawdopodobieństwo, że X≥190.

Wskazówka. Rozkład zmiennych X_i jest rozkładem Poissona z parametrem λ=2. Wiadomo, że w rozkładzie Poissona wartość oczekiwana jest równa λ i wariancja jest równa λ. Sformułować szczególny przypadek centralnego twierdzenia granicznego dla zmiennych X_i o rozkładzie Poissona z parametrem λ.

Statystyka matematyczna

Przedziały ufności

1. (Wstawiono plik przedział ufności dla średniej n- duże - Greń 1-18.)

Dla dużych n nie rozważamy zagadnienia konstruowania przedziałów ufności dla wariancji (lub, co na jedno wychodzi - dla odchylenia standardowego). Przyjmujemy natomiast zawsze, że z wystarczającą dokładnością nieznane sigma w populacji jest równe s otrzymanemu z próbki.

Dla małych n - konstruowanie przedziału ufności dla średniej i wartości - przykłady w odpowiednich plikach Excela (*.xls). Dla średniej: Korzysta się odpowiednio z rozkładu T Studenta (jeżeli sigma jest nieznane), lub z rozkładu normalnego - jeżeli sigma w populacji jest znane). Dla wariancji - korzysta się z rozkładu chi kwadrat.

Testowanie hipotez statystycznych dotyczących średniej i wariancji.

Teoria. Z populacji generalnej pobrano próbkę n-elementową (n - DUŻE, tzn. n>30) i otrzymano średnią próbkową
i wariancję próbkową s² względnie
. Zakładamy, że badana cecha X w populacji ma pewien rozkład posiadający wartość oczekiwaną i wariancję.

Testujemy hipotezę o średniej H₀:(m=m₀) przeciwko jednej z hipotez alternatywnych

a) H₁:(m≠m₀); b) H₁':(m>m₀); c) H₁'':(m<m₀).

Przyjmujemy, że z wystarczającą dokładnością σ≈s. Liczymy wartość statystyki
;

konstruujemy obszar krytyczny; dla poszczególnych przypadków jest to odpowiednio:

a) suma przedziałów (-∞,-u_α)∪(u_α,+∞), gdzie u_α wyznaczamy z tablic rozkładu normalnego z warunku Φ(u_α)=0,5-(α/2) względnie F(u_α)=1-(α/2); przez Φ rozumiemy tutaj pomocniczą funkcję związaną z dystrybuantą rozkładu normalnego, zdefiniowaną jako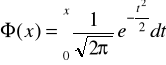
(dolną granicą całkowania jest zero; tablice tej funkcji - np. w zbiorze zadań Plucińska, Pluciński - charakteryzują się wartością 0 w zerze), zaś F jest dystrybuantą rozkładu normalnego N(0,1), czyli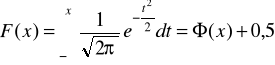
(dolną granicą całkowania jest -∞, tablice dystrybuanty, np. w skrypcie Eugenii Ciborowskiej - Wojdygi lub zbiorze zadań Jerzego Grenia charakteryzują się wartością 0,5 w zerze);

b) przedział (u_2α,+∞), gdzie u_2α wyznaczamy z warunku Φ(u_2α)=0,5-α względnie F(u_2α)=1-α;

c) przedział (-∞,-u_2α), gdzie u_2α ma to samo znaczenie, co w przypadku b).

Jeżeli wartość u_zaobs wpada do zbioru krytycznego, to hipotezę zerową H₀ odrzucamy na korzyść odpowiedniej hipotezy alternatywnej; w przeciwnym przypadku stwierdzamy jedynie, że nie ma podstaw do odrzucenia hipotezy H₀ na korzyść hipotezy alternatywnej.

(Uwaga. Nie omawiamy tutaj zagadnienia testowania hipotezy o wariancji w przypadku dużych n.)

1a. Z populacji generalnej pobrano próbkę n-elementową (n - MAŁE, tzn. n≤30) i otrzymano średnią próbkową
i wariancję próbkową s²_, względnie
. Zakładamy, że badana cecha X w populacji ma rozkład normalny. Testujemy hipotezę o średniej H₀:(m=m₀) przeciwko jednej z hipotez alternatywnych

a) H₁:(m≠m₀); b) H₁':(m>m₀); c) H₁'':(m<m₀).

Liczymy wartość statystyki
; konstruujemy obszar krytyczny; dla poszczególnych przypadków jest to odpowiednio:

a) suma przedziałów (-∞,-t_α)∪(t_α,+∞), gdzie t_α wyznaczamy z tablic rozkładu t Studenta o n-1 stopniach swobody.

b) przedział (t_2α,+∞), gdzie t_2α wyznaczamy z tablic rozkładu t Studenta o n-1 stopni swobody;

c) przedział (-∞,-t_2α), gdzie t_2α ma to samo znaczenie, co w przypadku b).

Jeżeli wartość t_zaobs wpada do zbioru krytycznego, to hipotezę zerową H₀ odrzucamy na korzyść odpowiedniej hipotezy alternatywnej; w przeciwnym przypadku stwierdzamy jedynie, że nie ma podstaw do odrzucenia hipotezy H₀ na korzyść hipotezy alternatywnej.

1b. Z populacji generalnej pobrano próbkę n-elementową (n - MAŁE) i otrzymano średnią próbkową i wariancję próbkową s²_, względnie . Zakładamy, że badana cecha X w populacji ma rozkład normalny. Testujemy hipotezę o wariancji H₀:(σ²=σ₀²) przeciwko hipotezie alternatywnej H₁:(σ²>σ₀²).

Liczymy wartość statystyki
; konstruujemy obszar krytyczny - ma on postać:

, gdzie
wyznaczamy z tablic rozkładu chi kwadrat o n-1 stopniach swobody. Jeżeli wartość
wpada do zbioru krytycznego, tzn.
, to hipotezę zerową H₀ odrzucamy na korzyść hipotezy alternatywnej H₁; w przeciwnym przypadku stwierdzamy jedynie, że nie ma podstaw do odrzucenia hipotezy H₀ na korzyść hipotezy alternatywnej.

Z tych samych statystyk i tych samych rozkładów korzystamy w celu skonstruowania przedziałów ufności (przy danym poziomie ufności) dla średniej lub wariancji (to ostatnie - tylko dla małych n).

1. (187 PP) Zużycie wody w fabryce w poszczególnych dniach podlega losowym wahaniom. Na podstawie pomiarów zużycia wody z n=365 dni roku stwierdzono, że średnie dzienne zużycie wody wynosi 102 m³, a średnie odchylenie kwadratów s² wynosi 81 (m⁶). a) Przyjmując poziom istotności α=0,02 zweryfikować hipotezę, że średnie dzienne zużycie wody wynosi 100 m³. b) Dla poziomów ufności 1-α wynoszących odpowiednio 0,9; 0,95; 0,98 i 0,99 skonstruować odpowiednie przedziały ufności dla średniej; c) Przyjmując poziom istotności α=0,05 przetestować hipotezę, że wariancja dziennego zużycia wody wynosi 60 (m⁶). d) Dla poziomów ufności 1-α wynoszących odpowiednio 0,9; 0,96 i 0,98 skonstruować odpowiednie przedziały ufności dla wariancji.

2. (189 PP) Wykonano pomiary mające na celu zbadanie głębokości oceanu. Pięć niezależnych pomiarów głębokości dało wyniki: 8,02 ; 8,01 ; 7,99 ; 8,03 ; 8,00 (km) . Przyjmujemy, że błędy pomiarów mają rozkład normalny. a) Na poziomie istotności α=0,01 przetestować hipotezę, że średnia głębokość wynosi 8,0 km. b) Zbudować 99 % przedział ufności dla średniej. c) Na poziomie istotności α=0,05 zweryfikować hipotezę, że wariancja wyników pomiarów wynosi 0,08 . d) Skonstruować 96 % przedziały ufności dla wariancji i odchylenia standardowego.

3. (193 PP) Zużycie energii elektrycznej przez pewien zakład przemysłowy w 10 kolejnych dniach wynosiło:

104; 100; 105; 110; 106; 105; 102; 107; 106; 105 (kWh). Zakładamy, że zużycie energii ma rozkład normalny. a) Zweryfikować hipotezę, że wariancja zużycia energii jest równa 4, przyjmując poziom istotności aa) α=0,1 ; ab) α=0,05 . b) Na poziomie ufności 0,9 skonstruować przedział ufności dla wariancji.

Test zgodności Pearsona - z danym rozkładem lub klasą rozkładów (zilustrowano licznymi przykładami w plikach Excela)

1. (199 PP) Liczby ocen niedostatecznych uzyskanych przez jednakowo liczne grupy studenckie na egzaminie podaje tabelka: (Grupa k - Liczba ocen niedostatecznych w grupie - n_k): 1-20; 2-16; 3-14; 4-14; 5-10; 6-16. Przyjmując poziom istotności α=0,05 zweryfikować hipotezę, że prawdopodobieństwa występowania ocen niedostatecznych w poszczególnych grupach są takie same (być może lepiej: że prawdopodobieństwa tego, iż losowo wybrana ocena niedostateczna będzie otrzymana przez studenta poszczególnej grupy, jest dla wszystkich grup takie samo, tzn. równe 1/6).

2. (201 PP) W ciągu 100 dni notowano liczby awarii sieci wodno - kanalizacyjnej w określonym rejonie miasta i uzyskano następujące dane liczbowe (Liczba awarii k - Liczba dni n_k): 0 - 10; 1 -27; 2 - 29; 3 - 19; 4 - 8; 5 - 7. Przyjmując poziom istotności α=0,05 zweryfikować hipotezę, że rozkład liczby awarii jest rozkładem Poissona.

3. (203 PP). Automat paczkuje kostki masła o nominalnej wadze 250 g. Zważono 200 kostek i uzyskano następujące wyniki (w przedziale od x' do x” znajduje się kostek): (248,0 - 248,4): 15; (248,4 - 248,8): 45; (248,8 - 249,2): 70; (249,2 - 249,6): 50; (249,6 - 250,0): 20. Przyjmując poziom istotności α=0,05 zweryfikować hipotezę, że waga kostek ma rozkład normalny.

4. Przeprowadzono n=200 serii po 6 niezależnych rzutów pewną monetą i otrzymano następujące wyniki

(ilość wyrzuconych orłów k - ilość serii, w których wyrzucono k orłów - n_k):

0 - 7; 1 - 18; 2- 45; 3 - 60; 4 - 46; 5 - 19; 6 - 5. Przyjmując poziom istotności α=0,10 zweryfikować hipotezę, że liczba orłów wyrzuconych tą monetą w serii rzutów ma rozkład dwumianowy z parametrem p=1/2 .

Dalsze przykłady na testowanie hipotez statystycznych oraz znajdowanie przedziałów ufności dla średniej i wariancji znajdują się w załączonych dokumentach w Excelu, gdzie można także podejrzeć zastosowane formuły.

Testowanie hipotezy o średniej - n-duże.

Testowanie hipotezy o średniej (sigma - nieznane) - n małe.

Brak przykładów: Testowanie hipotezy o średniej (sigma - znane) - n małe.

Testowanie hipotezy o wariancji (n-małe).

Przedział ufności dla średniej - n-duże.

Przedział ufności dla średniej i wariancji - n-małe.

Testowanie hipotezy o zgodności z danym rozkładem lub klasą rozkładów.

Analiza regresji i korelacji.

2

7

---