015(1)

Funkcja wykładnicza

Funkcja wykładnicza

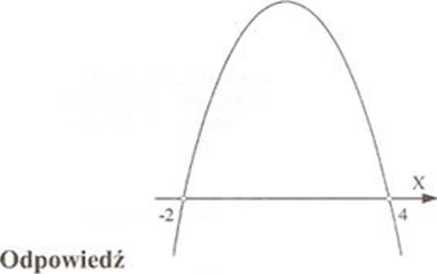
.v e (-00, -2) u (4, +x)

ZADANIE 6

, -3 I 3 irn < -

.» y

3 '. i < 3"¹

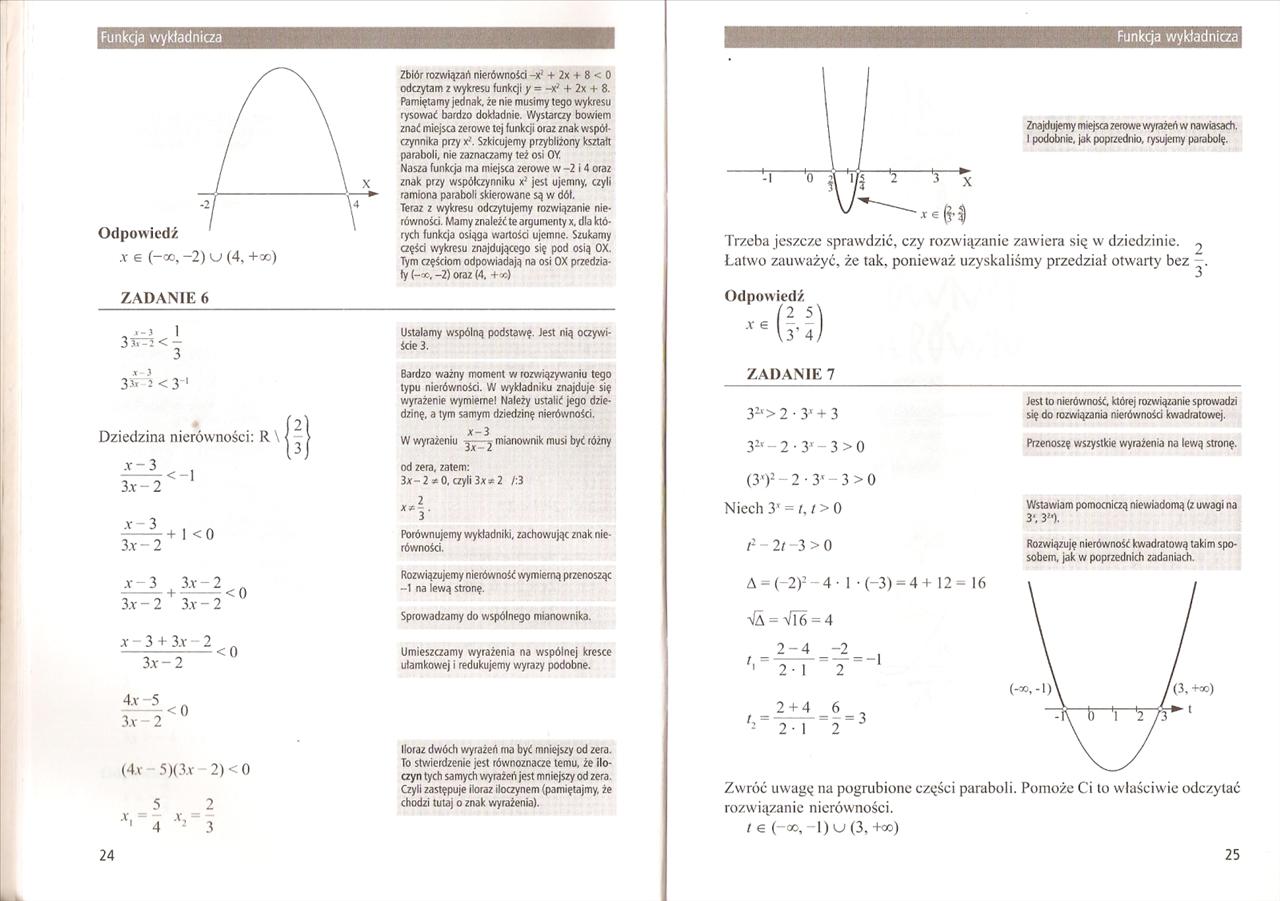
Zbiór rozwiązań nierówności -x^; + 2x + 8 < O odczytam z wykresu funkcji y =    + 2x + 8.

Pamiętamy jednak, że nie musimy tego wykresu rysować bardzo dokładnie. Wystarczy bowiem znać miejsca zerowe tej funkcji oraz znak współ czynnika przy xⁱ. Szkicujemy przybliżony kształt paraboli, nie zaznaczamy też osi OY Nasza funkcja ma miejsca zerowe w -2 i 4 oraz znak przy współczynniku x^ł jest ujemny, czyli ramiona paraboli skierowane są w dół.

Teraz z wykresu odczytujemy rozwiązanie nierówności. Mamy znaleźć te argumenty x. dla których funkcja osiąga wartości ujemne. Szukamy części wykresu znajdującego się pod osią 0X. Tym częściom odpowiadają na osi 0X przedziały (-x. -2) oraz (4. +«©)

Ustalamy wspólną podstawę. Jest nią oczywiście 3.

Dziedzina nierówności: R \

.r-3

3.v-2

<-l

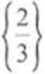
Bardzo ważny moment w rozwiązywaniu tego typu nierówności. W wykładniku znajduje się wyrażenie wymierne! Należy ustalić jego dziedzinę. a tym samym dziedzinę nierówności.

W wyrażeniu

Tir 2 ^m‘^an0vvn'*^{c mus}* 'óżny

od zera. zatem:

3x-2 *0, czyli 3x* 2 /:3

.y- 3 3.v-2

+ I <0

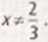
Poróv/nujemy wykładniki, zachowując znak nie równości.

■V- 3 _f 3*-2 3.v-2 ⁺ 3.Y-2

<0

,y - 3 + 3.v - 2 3.v-2

<0

Rozwiązujemy nierówność wymierną przenosząc -1 na lewą stronę.

Sprowadzamy do wspólnego mianownika.

Umieszczamy wyrażenia na wspólnej kresce ułamkowej i redukujemy wyrazy podobne.

-5

— < y 2

(4.v 5)(3.y 2) < 0

5    2

X, .v.    ;

Iloraz dwóch wyrażeń ma być mniejszy od zera. To stwierdzenie jest równoznacze temu. że iloczyn tych samych wyrażeń jest mniejszy od zera. Czyli zastępuje iloraz iloczynem (pamiętajmy, że chodzi tutaj o znak wyrażenia).

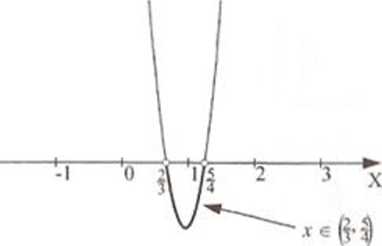
Znajdujemy miejsca zerowe wyrażeń w nawiasach. I podobnie, jak poprzednio, rysujemy parabolę.

Trzeba jeszcze sprawdzić, czy rozwiązanie zawiera się w dziedzinie. ₀ Łatwo zauważyć, że tak. ponieważ uzyskaliśmy przedział otwarty bez

Odpowiedź

'*(!■!)

ZADANIE 7

3^2l > 2 • 3‘ + 3

Jest to nierówność, której rozwiązanie sprowadzi się do rozwiązania nierówności kwadratowej.

3^2r — 2 * 3^X — 3 > 0

Przenoszę wszystkie wyrażenia na lewą stronę.

(3')² 2-3’ 3 > 0 Niech 3* = /, t > 0

Wstawiam pomocniczą niewiadomą (z uwagi na 3*. 3'0.

A = ( 2)^: 4- I (-3) = 4+ 12= 16 Va = VT6 = 4

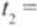
2 + 4 2- I

6

2

3

Rozwiązuję nierówność kwadratową takim sposobem, jak w poprzednich zadaniach.

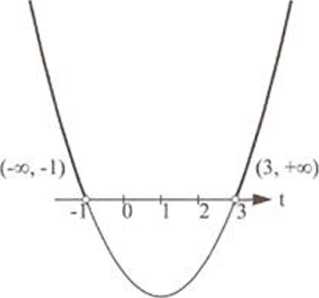
Zwróć uwagę na pogrubione części paraboli. Pomoże Ci to właściwie odczytać roz w iąza n i e n i erówtiośc i.

/ € (-oo, I) u (3. +co)

25