13727 img477 (2)

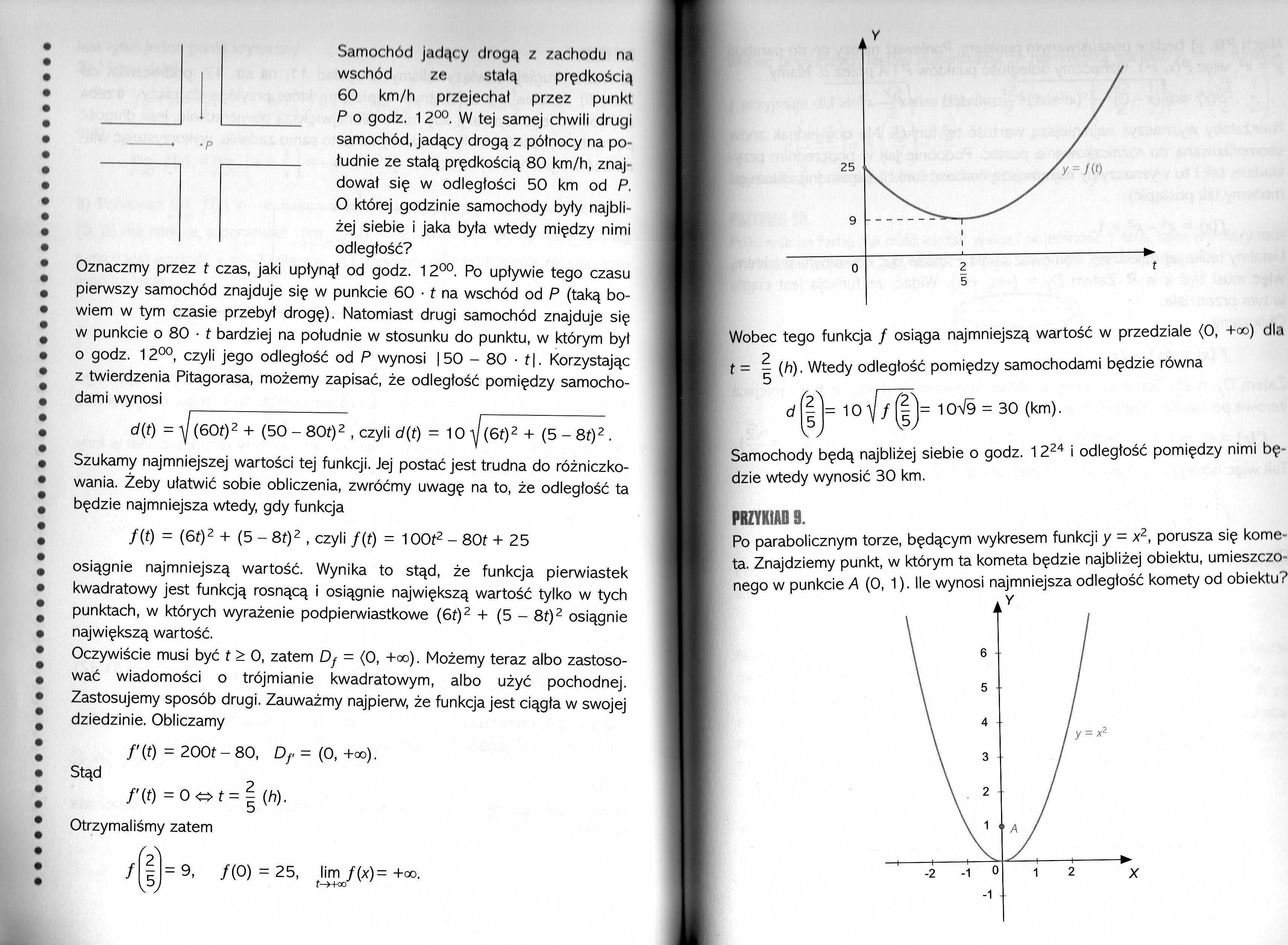
Samochód jadący drogą z zachodu na wschód ze stałą prędkością 60 km/h przejechał przez punkt

__P o godz. 12⁰⁰. W tej samej chwili drugi

,    .,    samochód, jadący drogą z północy na po-

_ _ łudnie ze stałą prędkością 80 km/h, znajdował się w odległości 50 km od P. O której godzinie samochody były najbliżej siebie i jaka była wtedy między nimi odległość?

Oznaczmy przez t czas, jaki upłynął od godz. 1 2⁰⁰. Po upływie tego czasu pierwszy samochód znajduje się w punkcie 60 • t na wschód od P (taką bowiem w tym czasie przebył drogę). Natomiast drugi samochód znajduje się w punkcie o 80 ■ t bardziej na południe w stosunku do punktu, w którym był o godz. 12⁰⁰, czyli jego odległość od P wynosi | 50 - 80 • t\. Korzystając z twierdzenia Pitagorasa, możemy zapisać, że odległość pomiędzy samochodami wynosi

d(t) = ]/(60t)² + (50-80f)² , czyli d(t) = 10 ]/(6t)² + (5-81)² .

Szukamy najmniejszej wartości tej funkcji. Jej postać jest trudna do różniczkowania. Żeby ułatwić sobie obliczenia, zwróćmy uwagę na to, że odległość ta będzie najmniejsza wtedy, gdy funkcja

f(t) = (61)² + (5 - 8f)² , czyli f(t) = 1001² - 801 + 25

osiągnie najmniejszą wartość. Wynika to stąd, że funkcja pierwiastek kwadratowy jest funkcją rosnącą i osiągnie największą wartość tylko w tych punktach, w których wyrażenie podpierwiastkowe (6f)² + (5 - 81)² osiągnie największą wartość.

Oczywiście musi być t > 0, zatem Df = (0, +oo). Możemy teraz albo zastosować wiadomości o trójmianie kwadratowym, albo użyć pochodnej. Zastosujemy sposób drugi. Zauważmy najpierw, że funkcja jest ciągła w swojej dziedzinie. Obliczamy

f'(f) = 200f- 80, Df = (0, +oo).

Stąd

f'(t) = 0of = | (h).

Otrzymaliśmy zatem

V⁵?

= 9,    /(O) = 25, lim /(x)= +oo.

f->+00

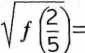
10^9 = 30 (km).

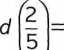
10

y

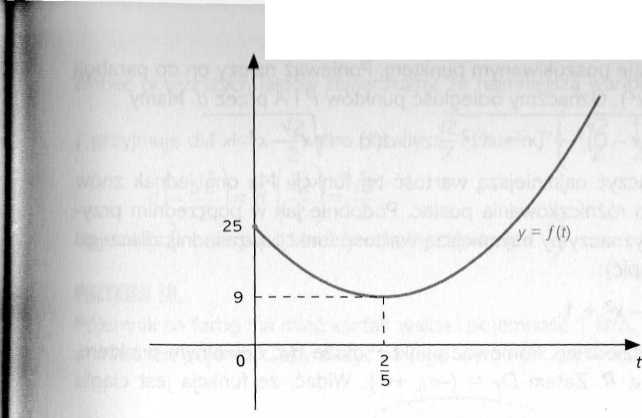
Wobec tego funkcja / osiąga najmniejszą wartość w przedziale (O, +oo) dla 2

f = - (h). Wtedy odległość pomiędzy samochodami będzie równa

w

Samochody będą najbliżej siebie o godz. 1 2²⁴ i odległość pomiędzy nimi będzie wtedy wynosić 30 km.

PRZYKtAB 9.

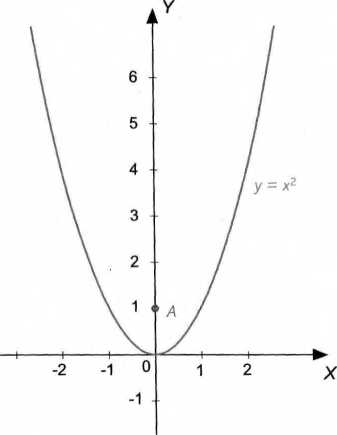
Po parabolicznym torze, będącym wykresem funkcji y = x², porusza się kometa. Znajdziemy punkt, w którym ta kometa będzie najbliżej obiektu, umieszczonego w punkcie A (0, 1). Ile wynosi najmniejsza odległość komety od obiektu?