20425 Obraz (1523)

I M ks/iiiltowuiiii' struktury kiipllalu |*i/i'il^,ik^,l>lnr.l\vii

•    indywidualne ciekły regulacji rządowych, np. dotyczących ochrony środowiska

•    konkurencja krajowa i zagraniczna;

•    poziom dźwigni operacyjnej i finansowej stosowany przez przedsiębiorstwo;

•    polityka w zakresie zatrudnienia.

Ryzyko niesystematyczne może w znacznej części być wyeliminowane przez efektywnie zdywersyfikowany portfel inwestycyjny. Stanowi ono niekiedy 5(L’i i więcej ryzyka całkowitego, a zatem jego dywersyfikacja może przynieść znaczące efekty.

Ważna dla analizy ekonomicznej relacja ryzyko-zwrot może zostać przed stawiona w postaci linii prostej, nazywanej linią rynku papierów wartościowych (SML — Security Market Linę). Prezentuje ona relacje między ryzykiem sys tematycznym a oczekiwanym zwrotem (oczekiwanym dochodem a współczyn nikiem beta), występujące na danym rynku kapitałowym. Linia ta jest przedstawiona na rysunku 5.1.

Rysunek 5.1 Linia SML

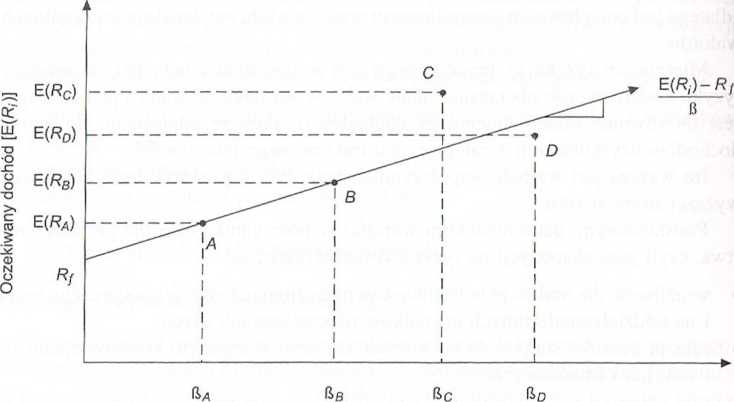
Współczynnik beta (H)

Źródło: J.M. Samuels. F.M. Wilkes, R.E. Brayshaw, 1995, s. 263.

Linia SML wiąże ryzyko mierzone przez współczynnik beta z oczekiwaną lub wymaganą stopą zwrotu z danego papieru wartościowego. Uważa się, że prosta ta wyraża cenę rynkową ryzyka lub, inaczej, dodatkowy oczekiwany zwrot, który zostanie zrealizowany przez poniesienie dodatkowej jednostki ryzyka. Pozwala ona też znaleźć stopę dyskonta dla inwestycji, a więc koszt kapitału, wyznaczając

minimalną efektywność rozważanych projektów inwestycyjnych przy założonym |in/iomic ryzyka, jak również wskazuje walory nadmiernie wycenione i nie dnv/.ncowane przez rynek kapitałowy. Znajomość SML umożliwia określenie opłacalności poszczególnych inwestycji.

Równanie prostej SML, będącej modelem wyceny aktywów kapitałowych ii APM), jest następujące:

VM<_r) = Rj+[E (R_m)-Rj] X ft,

gdzie:

M/ć,,) — spodziewana stopa zwrotu z portfela leżącego na SML,

R,    — stopa procentowa pozbawiona ryzyka,

L {!<„,) — oczekiwana stopa zwrotu z portfela rynkowego,

|l,    — współczynnik beta.

Wynika z tego, że oczekiwany zwrot tworzą:

•    wartość pieniądza w czasie (Rj);

•    nagroda za ponoszenie ryzyka systematycznego, czyli rynkowa premia za ryzyko (nachylenie prostej SML, tj. różnica między oczekiwanym dochodem z portfela rynkowego a stopą wolną od ryzyka [E (/?,„) — /?,]);

•    wielkość ryzyka systematycznego (3,.

Przykład 5.4

Stopa wolna od ryzyka wynosi 6%, premia tynkowa 10,4%, a współczynnik beta danego waloru to 1,2. Obliczyć zwrot z tego waloru, wykorzystując model CAPM.

E(R_P) = R/+ [E (/?,„)-/?/] x (3, ,

6% + 10,4% x 1,2 = 6% + 12,48% = 18,48%.

Podstawową zależność między ryzykiem a dochodem z inwestycji A i B można przedstawić w sposób następujący:

EOO-R, ₌ E (Rb) - R/

Równanie to wskazuje, że na efektywnym rynku kapitałowym wskaźnik premia do ryzyka (PR/R) musi być jednakowy dla wszystkich instrumentów finansowych na nim występujących, a zatem wszystkie one muszą leżeć na tej samej prostej. Walory A i B leżące na tej samej linii muszą mieć takie same wskaźniki PR IR. Jeśli jakiś instrument znalazłby się powyżej prostej SML (C), jego cena wzrastałaby, a wraz z tym wzrostem malałby oczekiwany dochód, aż do momentu, kiedy instrument ten znalazłby się dokładnie na tej prostej. Podobnie jeśli jakiś instrument znalazłby się poniżej prostej (D), oczekiwane dochody z takiego instrumentu wzrastałyby aż do momentu, kiedy znalazłby się on na prostej. A zatem wskaźnik premia-ryzyko dla