24711 skanuj0151 (11)

282

B. Cieślar

\fi

u

*4-r⁰T+-®~

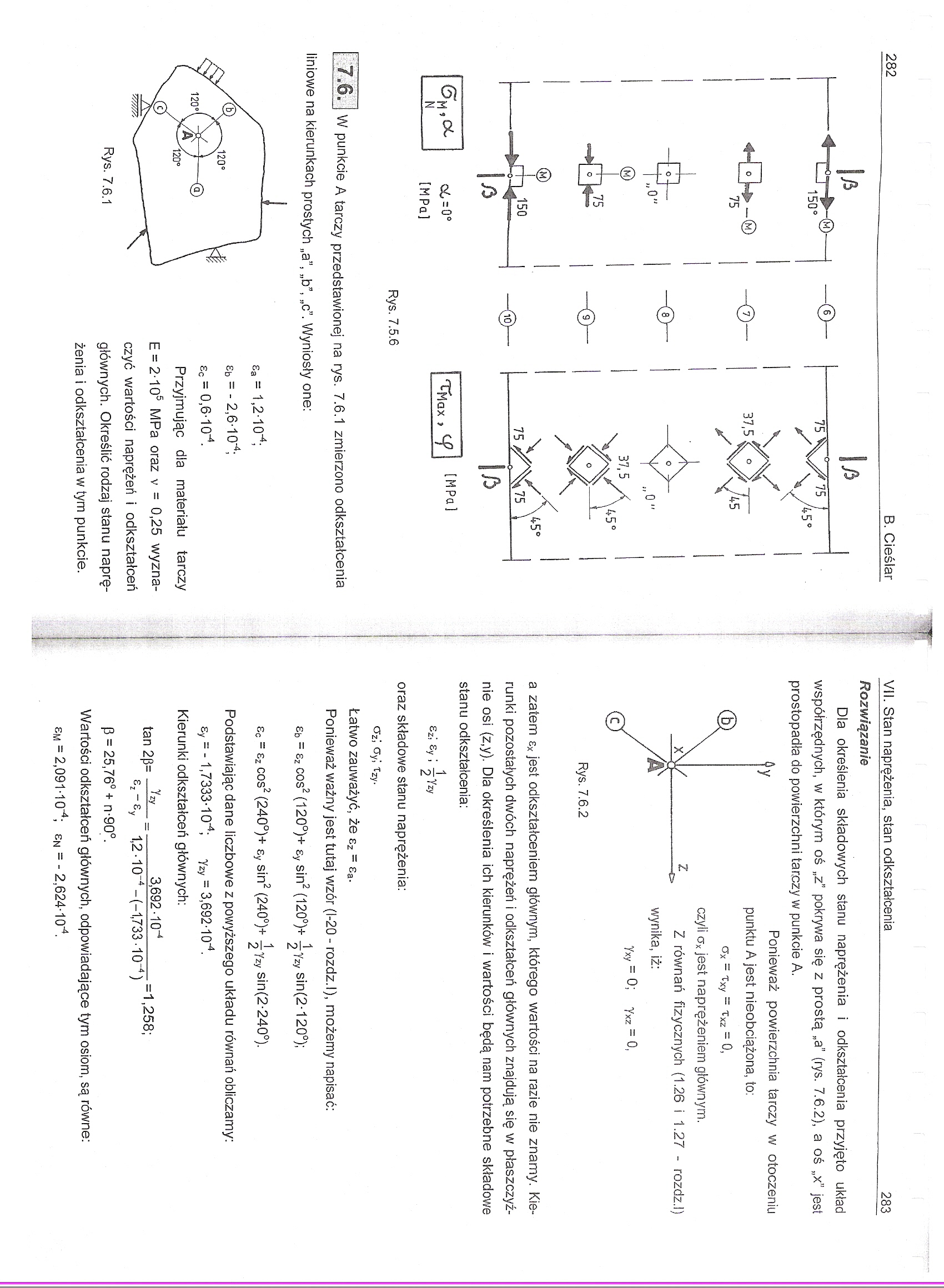
¹—¹ 150°

75

,0"

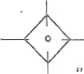
0"

V ³⁷'⁵

.75

150

|/i>

	oC=0°
N	[MPa]

Rys. 7.5.6

[MPa]

:7»6fe W punkcie A tarczy przedstawionej na rys. 7.6.1 zmierzono odkształcenia

liniowe na kierunkach prostych „a”, „b”, „c”. Wyniosły one:

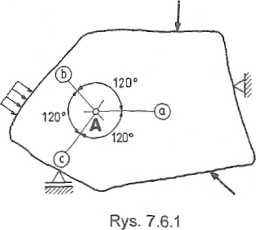
s_a = 1,2-1 O*⁴;

E_b = - 2,6-10"⁴;

Sc = 0,6-10-⁴.

Przyjmując dla materiału tarczy E = 2-10⁵ MPa oraz v = 0,25 wyznaczyć wartości naprężeń i odkształceń głównych. Określić rodzaj stanu naprężenia i odkształcenia w tym punkcie.

Rozwiązanie

Dla określenia składowych stanu naprężenia i odkształcenia przyjęto układ współrzędnych, w którym oś „z" pokrywa się z prostą „a” (rys. 7.6.2), a oś „x” jest prostopadła do powierzchni tarczy w punkcie A.

Ponieważ powierzchnia tarczy w otoczeniu punktu A jest nieobciążona, to:

Ox ⁼ Txy ⁼ ^xz ⁼ 0,

czyli a_x jest naprężeniem głównym.

Z równań fizycznych (1.26 i 1.27 - rozdz.l) wynika, iż:

Yxy = 0; Yxz = 0, a zatem s_x jest odkształceniem głównym, którego wartości na razie nie znamy. Kierunki pozostałych dwóch naprężeń i odkształceń głównych znajdują się w płaszczyźnie osi (z,y). Dla określenia ich kierunków i wartości będą nam potrzebne składowe stanu odkształcenia:

e_z; ^£y I 2^

oraz składowe stanu naprężenia:

Cfzi Oy! ^zy-

Łatwo zauważyć, że e_z = s_a.

Ponieważ ważny jest tutaj wzór (I-20 - rozdz.l), możemy napisać: s_b = 8_Z cos² (120°)+ s_y sin² (120°)+ ^y_zy sin(2-120°);

s_c = s₂ cos² (240°)+ s_y sin² (240°)+ ^Yzy sin(2-240°).

Podstawiając dane liczbowe z powyższego układu równań obliczamy: Sy = -1,7333-1 O*⁴:    Yzy = 3,692-10^-4.

Kierunki odkształceń głównych:

tan 2(3=

-=1,258;

Yzy__3,692-10"⁴

s_y 1,2 -10 - (-1,733 ■ 10^-4) p = 25,76° + n-90°.

Wartości odkształceń głównych, odpowiadające tym osiom, są równe: s_M = 2,091 -10^-4; sn = - 2,624-10^-4.