23071 Obraz (2401)

39, Środek masy układu punktów materialnych HJPM).
Oxyz - układ bezwładnościowy,
C - środek masy, mi, m2, rrij - masy składowe, mc - sumaryczna masa, rc[xc, yc, zc] - składowe wektora położenia środka masy.
Poszukiwanie środka masy punktów materialnych:
n
=2>,
/-1
środkiem masy układu punktów materialnych nazwiemy taki punkt C, którego promień - wektor rc poprowadzony z poprzednio obranego bieguna O określony jest z pomocą następującego równania:
i=n
„ _ i=l_
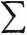
i-1
m,
Promień - wektor środka masy równy jest sumie geometrycznej iloczynów mas i promieni - wektorów PM rozpatrywanego układu, podzielonej przez sumę mas wszystkich tych punktów.
90. Współrzędne prostokątne środka masy UPM.
Oxyz - układ bezwładnościowy,
C - środek masy, m,, m2, ntj - masy składowe, mc - sumaryczna masa, rc[xc, yc, Zc] - składowe wektora położenia środka masy.
Środkiem masy układu punktów materialnych nazwiemy taki punkt C, którego promień - wektor rc poprowadzony z poprzednio obranego bieguna O określony jest z pomocą następującego równania:
i=n
'r>
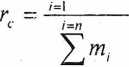
i=I
Promień - wektor środka masy równy jest sumie geometrycznej iloczynów mas i promieni - wektorów PM rozpatrywanego układu, podzielonej przez sumę mas wszystkich tych punktów.
Oznaczmy przez x„ y0, zc współrzędne prostokątne środka masy C, równe składowym jego promienia - wektora rc poprowadzonego z początku O układu współrzędnych. Z powyższego równania otrzymujemy bezpośrednio:
=
i=i
i-n
i=\
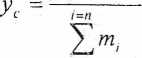
/=[
27
Wyszukiwarka
Podobne podstrony:
Slajd7 3 Środek masy układu punktów materialnych gdzie m - masa całkowita układu:
= lim xdm 1 f , -= — J xdm 1dm M X źr.m. Środek masy układu punktów materialnych pomsza się w taki
Zasady zmienności w dynamice układu punktów materialnych i ciała sztywnego. Środek masy. Momenty
skrypt wzory i prawa z objasnieniami32 62Środek masy ■ Wzory określające położenie środka masy układ
mechanika128 rosi krętu układu punktów materialnych względem środka masy C jest równy pokrętowi mome
mechanika128 rosi krętu układu punktów materialnych względem środka masy C jest równy pokrętowi mome
Obraz (2400) 91. Pojecie momentów statycznych. Oxyz - układ bezwładnościowy, C - środek masy, mi, m2
IMAG0075 1 Uzupełnij wzór i opisz użyte symbole Kręt układu punktów materialnych m
Slajd27 2 Zasada krętu układu punktów materialnych 27
Slajd41 Zasada równoważności energii kinetycznej i pracy dla układu punktów materialnych 41
Kręt układu punktów materialnych Ruch układu o zmiennej masie Definicja i równania pracy mechaniczne
7.5 Prawo zmienności energii kinetycznej układu punktów materialnych ...................227 7.6
Obrazek 01 dynamika -temat 3 Wy korzy snując równania opisujące zjawisko ruchu układu punktów materi
materialnych, pęd i energia układu punktów materialnych, zasada zachowania pędu i energii mechaniczn
więcej podobnych podstron