278 279

1.6. (100011111)_gpay

1.7.    (1613)₈.

1.8.    (12202)₄.

1*9. Jeden z możliwych kodów przedstawiono na rys. R.3*

Dla tego kodu można stwierdzić, że nadano:

a)    to samo co odebrano (nie wystąpił błąd) bo ilość jedynek w poszczególnych grupach jest parzysta,

b)    001101001011001 (błąd w pierwszym bicie).

^x«

^x«

X,

^x»

^x7

H

^XJ

^XA

^XJ

*1

^X1

h

Dl

Si

GRUPA 1

X

X

X

X

X

X

X

X

GRUPA 2

X

X

X

X

X

X

X

X

GRUPA 3

X

X

X

X

X

X

X

X

GRUPA l*

X

X

X

X

X

X

X

X

Rys. R.3. Kod Hamminga do zadania 1.9

1.10.	(+18>10	(-18)10	(+7)10	1 -i o
zn-moduł	010010	110010	000111	100111
zn-uz.do 1	010010	101101	000111	111000
zn-uz.do 2	010010	101110	000111	111001
1.11. a) 1110,1001; b) 1001,11;		c) 11001 i	d) 1011
1.12. a) 011001;	001011; 101011;	111001
b) 011001;	001011; 110100;	100110
c) 011001;	001011; 110101;	100111

1.13.    a) x, b) xy+ z, c) xy+ ź

1.14.    f(x,y,z)= n(2,5)

1.15.1(0,2,3,6,(4))

1.16.    Nie będzie pogody lub pójdę na spacer.

1.17.    Zawsze.

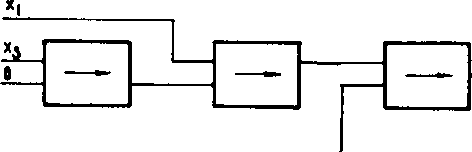
1.20. Patrz rys. R.4.

Rys. R.4. Schemat do zadania 1.20

1.21. Patrz rys. R.5. p(x,y,z,w)=£ (0,1,2,4,5,10,11,12)

O

1.22.£(0,1,2,7)

2.1.    a) f =    + x₁x₂x_if + x₁x₂x^ + x^x₂x^ =

= (x₁₊x₂₊x₃) (x₁+x₂+x_ił) (x₁+x₂+5c₃ ) (x₁+x₂+x₄)

bj f = x₁x₂x₃x_ifx₃ + x^x₂x^ + XtX_uX^ + X₂X^ s

= (x₂+x₄+x₅)(x₂+x₃+x₄}(x₂+x₃)(5Ei+x_if)[(x₃-ł-x₄+x₅) albo (x₂+x₃+x^j

c)    f = x₃x₄x₅+x₁x₃x₅ = (x₃+5E₄)(x₁+x₃)x₃

d)    t = x₂x₃x₄+x₁x₃x₃+x₂x₄5E₃ =

= (x₃+x₄+x₃)(x₁+x₃)x₂[(x₃+x₄+x₃) albo (x₁+x₃+x₄)]

2.2.    f = BSD (patrz rys. R.6)

2.3.    (i = x₁x₃+x₂x₃x₄+x₁x₂x₃

2.4.    f = i₁i₂x₂+s₁s₂x₁+I₁5₃+x₂x₃+s₁s₂x₁x₂x₃

2.5.    Patrz rys. R.7.

ł